题目内容
如图，直线y＝kx＋b经过点A(5，0)，B(1，4)．
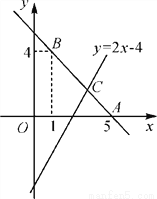
（1）求直线AB的表达式；
（2）若直线y＝2x－4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式kx＋b＞2x－4>0的解集．
（1）y=-x+5；（2）C（3，2）；（3）2
优质课堂快乐成长系列答案如图，在Rt△ABC中，∠C=90°，BD是∠ABC的平分线，交AC于点D，若CD=n，AB=m，则△ABD的面积是（ ）
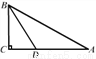
A. mn B.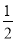 
mn C. 2mn D. 
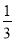mn
B
【解析】
作DE⊥AB交AB于点E，
∵BD是∠ABC的平分线，∠C=90°，
∴CD=DE=n，
∴S△ABD=AB·DE=mn.
故选B. （2x-1）2等于（ ）
A. 4x2-4x+1 B. 2x2-2x+1 C. 2x2-1 D. 2x2+1
A
【解析】根据完全平方公式可得：（2x-1）2=4x2-4x+1 ，故选A. (y+3z)(3z-y)等于（ ）
A. y2-z2 B. y2-9z2 C. 9z2-y2 D. y2-z2
C
【解析】根据平方差公式可得：(y+3z)(3z-y)=9z2-y2，故选C. （x+5y）（x-5y）等于（ ）
A. x2-5y 2 B. x2-y 2 C. x2-25y 2 D. 25x2-y 2
C
【解析】根据平方差公式可得：（x+5y）（x-5y）=x2-25y 2 ，故选C. 如图，点A2，A4…分别是x轴上的点，点A1，A3，A5，…分别是射线OA2n-1上的点，△OA1A2，△OA2A3，△OA3A4，…分别是以OA2，OA3，OA4 ，OA5…为底边的等腰三角形，若OA2n-1与x轴正半轴的夹角为30°，OA1=1，则可求得点A2的坐标是________；A2n-1的坐标_______.
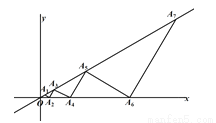
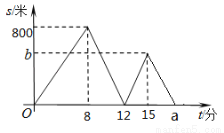
【解析】根据等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,再由等腰三角形的三线合一的性质和30°角直角三角形的性质可求得， ，由此可得A2n-1的坐标. 小明、小宇从学校出发到青少年宫参加书法比赛，小明步行一段时间后，小宇骑自行车沿相同路线行进，两人均匀速前行．他们的路程差s（米）与小明出发时间t（分）之间的函数关系如图所示．下列说法：①小宇先到达青少年宫；②小宇的速度是小明速度的3倍；③a=20；④b=600．其中正确的是（ ）
A．①②③ B．①②④ C．①③④ D．①②③④
B．
【解析】
试题分析：由图象得出小文步行720米，需要9分钟，
所以小文的运动速度为：720÷9=80（m/分），
当第15分钟时，小亮运动15-9=6（分钟），
运动距离为：15×80=1200（m），
∴小亮的运动速度为：1200÷6=200（m/分），
∴200÷80=2.5，（故②正确）；
当第19分钟以后两人之间距离越来越近，说明小亮已... 一项工程，甲单独做需要x小时完成，乙单独做需要y小时完成，则两人一起完成这项工程需要_______小时.
【解析】设该工程总量为1．二人合作完成该工程所需天数=1÷（=． 根据变化完成式子的变形：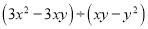 
＝3x÷_____．
y
【解析】因为,故答案为: y.