题目内容
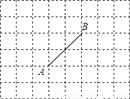
在所给的8×6网格图中,横竖每相邻两点间的长度均为1,以这些点为顶点的三角形称为网格三角形,请找出点M,使以A,B,M为顶点的网格三角形是直角三角形,这样的点M有_______个.
 12
【解析】如图,在线段CD和线段EF上各有5个符合条件的点,图中的两个M点也符合要求,所以符合条件的点M共有12个.
12
【解析】如图,在线段CD和线段EF上各有5个符合条件的点,图中的两个M点也符合要求,所以符合条件的点M共有12个.
如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )

A. 1处 B. 2处 C. 3处 D. 4处
 D
【解析】如图A、B、C、D为三条直线组成的三角形内角和外角的角平分线的交点,由角平分线上的点到角两边距离相等可得在这四点处,货物中转站到三条公路距离相等.
故选D.
D
【解析】如图A、B、C、D为三条直线组成的三角形内角和外角的角平分线的交点,由角平分线上的点到角两边距离相等可得在这四点处,货物中转站到三条公路距离相等.
故选D. (a+2b+2c)(a+2b-2c)等于_______;
 【解析】(a+2b+2c)(a+2b-2c)=(a+2b)2-4c2=.
【解析】(a+2b+2c)(a+2b-2c)=(a+2b)2-4c2=. (m+5)(m-5)等于( )
A. m2-5 B. m2-y 2 C. m2-25 D. 25m2-5
 C
【解析】根据平方差公式可得:(m+5)(m-5)=m2-25,故选C.
C
【解析】根据平方差公式可得:(m+5)(m-5)=m2-25,故选C. 如图,在平面直角坐标系内,四边形OECB的顶点坐标分别是:B(2,5),C(8,5),E(10,0),点P(x,0)是线段OE上一点,设四边形BPEC的面积为S.
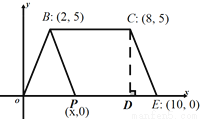
(1)过点C作CD⊥x轴于点E,则CD= , 用含x的代数式表示PE= .
(2)求S与x的函数关系.
(3)当S=30时,直接写出线段PE与PB的长.
 (1)CD=5,PE=10-x;(2)(3)PE=6,PB=
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,P...
(1)CD=5,PE=10-x;(2)(3)PE=6,PB=
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,P... 对于平面直角坐标系中任意两点M(x1, y1),N(x2,y2),称|x1﹣x2|+|y1﹣y2|为M,N两点的勾股距离,记作:d(M,N).如:M(2,﹣3),N(1,4),则d(M,N)=|2-1|+|-3-4|=8. 若P(x0,y0)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P,Q)的最小值为P到直线y=kx+b的勾股距离.则P(-3,2)到直线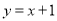 的勾股距离为( )
的勾股距离为( )
A. 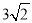 B.
B. 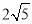 C. 3 D. 4
C. 3 D. 4
 D
【解析】根据垂线段最短,可得当PQ直线时,PQ最短,设PQ 的解析式为y=-x+b,把P(-3,2)代入求得b=-1,所以PQ 的解析式为y=-x-1,令-x-1=x+1,解得x=-1.把x=-1代入y=x+1得y=0,即可得点Q的坐标为(-1,0),所以P(-3,2)到直线的勾股距离为|-3﹣(-1))|+|2﹣0|=2+2=4,故选D.
D
【解析】根据垂线段最短,可得当PQ直线时,PQ最短,设PQ 的解析式为y=-x+b,把P(-3,2)代入求得b=-1,所以PQ 的解析式为y=-x-1,令-x-1=x+1,解得x=-1.把x=-1代入y=x+1得y=0,即可得点Q的坐标为(-1,0),所以P(-3,2)到直线的勾股距离为|-3﹣(-1))|+|2﹣0|=2+2=4,故选D. 平面直角坐标系内有一点A(2,﹣3),则点A位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
 D
【解析】因点A的横坐标为正,纵坐标为负,所以点A位于第四象限,故选D.
D
【解析】因点A的横坐标为正,纵坐标为负,所以点A位于第四象限,故选D. 下列式子是分式的是( )
A. 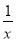 B.
B. 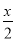 C.
C. 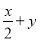 D.
D. 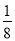
 A
【解析】根据分母中含有字母的式子是分式,即可进行判断.
【解析】
式子, , 的分母中不含有字母,是整式;式子的分母中含有字母,是分式.
故选A.
A
【解析】根据分母中含有字母的式子是分式,即可进行判断.
【解析】
式子, , 的分母中不含有字母,是整式;式子的分母中含有字母,是分式.
故选A. 若x=-1,y=2,则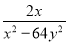 -
-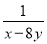 的值为( )
的值为( )
A. -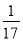 B.
B. 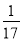 C.
C. 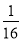 D.
D. 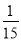
 D
【解析】试题分析:原式====,
当, 时,原式==.故选D.
D
【解析】试题分析:原式====,
当, 时,原式==.故选D. 
