��Ŀ����
��ģ�ͽ�����
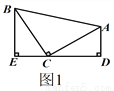
��1����ͼ1������ֱ��������ABC�У���ACB=90�㣬CB=CA��ֱ��ED������C����A��AD��ED�ڵ�D����B��BE��ED�ڵ�E����֤����BEC�ա�CDA��
��ģ��Ӧ�á�
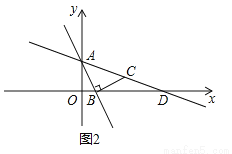
��2����ͼ2��һ�κ���y=��2x+2��ͼ����y�ύ�ڵ�A����x�ύ�ڵ�B������B���߶�BC��AB��BC=AB��ֱ��AC��x���ڵ�D��
�����C�����꣬��ֱ��д��ֱ��AC�ĺ�����ϵʽ��
������Q��ͼ2������ƽ����һ�㣬���Ե�A��D��QΪ������������ǵ���ֱ��������ʱ��ֱ��д����Q������.
 ��1��֤����������
��2���٣���
�����������������
��1��֤����������
��2���٣���
�����������������
�������С�B��ƽ���ߺ���ǵ�ƽ���ߵļн��ǣ� ����
A. 60�� B. 90�� C. 45�� D. 135��
 B
��������
��ͼ��BDƽ�֡�ABF��BEƽ�֡�ABC��
���ABD=��ABF����ABE=��ABC��
���DBE=��DBA+��ABE=��ABF+��ABC=����ABF+��ABC��=90��.
��ѡB.
B
��������
��ͼ��BDƽ�֡�ABF��BEƽ�֡�ABC��
���ABD=��ABF����ABE=��ABC��
���DBE=��DBA+��ABE=��ABF+��ABC=����ABF+��ABC��=90��.
��ѡB. ��x+5y��2 ���ڣ� ��
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
 C
��������������ȫƽ����ʽ�ɵã���x+5y��2=x2+10xy+25y 2 ����ѡC.
C
��������������ȫƽ����ʽ�ɵã���x+5y��2=x2+10xy+25y 2 ����ѡC. [c+��a2)2][c-��a2)2]���ڣ� ��
A. c -a2 B. c2 -a8 C. c2 -a2 D. c2 -a4
 B
������������ƽ���ʽ���ݵij˷�����ɵã�[c+��a2)2][c-��a2)2]= =c2 -a8����ѡB.
B
������������ƽ���ʽ���ݵij˷�����ɵã�[c+��a2)2][c-��a2)2]= =c2 -a8����ѡB. ��2x+y 2 ����2x-y 2 �����ڣ� ��
A. x2-y 4 B. x2-y 2 C. 4x2-y4 D. 4x2-y 2
 C
������������ƽ���ʽ�ɵã���2x+y 2 ����2x-y 2 ��=4x2-y4 ����ѡC.
C
������������ƽ���ʽ�ɵã���2x+y 2 ����2x-y 2 ��=4x2-y4 ����ѡC. ��ͼ��  �ĵ㹲�ߣ�
�ĵ㹲�ߣ� 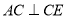 ��
�� 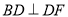 ��
�� 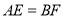 ��
�� 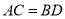 .��֤��CE��DF.
.��֤��CE��DF.
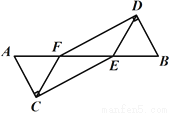
 ֤��������.
���������������������HL֤��Rt��ACE?Rt��BDF������ȫ�������ε����ʼ��ɵá�AEC=��BFD�����ڴ�����ȣ���ֱ��ƽ�м��ɵ�CE��DF.
���������
��AC��CE,BD��DF��
���ACE=��BDF=90�㣬
�֡�AE=BF,AC=BD��
��Rt��ACE?Rt��BDF(HL)��
���AEC=��BFD��
��CE��DF.
...
֤��������.
���������������������HL֤��Rt��ACE?Rt��BDF������ȫ�������ε����ʼ��ɵá�AEC=��BFD�����ڴ�����ȣ���ֱ��ƽ�м��ɵ�CE��DF.
���������
��AC��CE,BD��DF��
���ACE=��BDF=90�㣬
�֡�AE=BF,AC=BD��
��Rt��ACE?Rt��BDF(HL)��
���AEC=��BFD��
��CE��DF.
... ��֪��M��2m -3,8����N��m -1,-3������MN//y�ᣬ��m=________.
 2
����������MN//y�ᣬ�ɵõ�M��N�ĺ�������ͬ����2m-3=m-1�����m=2.
2
����������MN//y�ᣬ�ɵõ�M��N�ĺ�������ͬ����2m-3=m-1�����m=2. ��֪��ʽ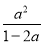 ��
��
��1����____ʱ����ʽ��ֵ�����㣻
��2����____ʱ����ʽ�����壻
��3����___��___ʱ��ʽ��ֵ��������
��4����____ʱ����ʽ��ֵ�Ǹ�����
 ����������1�����ݷ�ʽֵΪ��������ɵ�a2=0����1-2a��0���ٽ⼴�ɣ�
��2�����ݷ�ʽ������������ɵ�1-2a=0���ٽⷽ�̼��ɣ�
��3�����ݷ�ʽֵΪ���ɵ÷��ӷ�ĸΪͬ�ţ����1-2a>0����a��0���ٽⲻ��ʽ���ɣ�
��4�����ݷ�ʽֵΪ���ɵ÷��ӷ�ĸΪ��ţ����1-2a<0����a��0���ٽⲻ��ʽ���ɣ�
��������
(1)������ã�a2=0����1?2a��0��
��ã�...
����������1�����ݷ�ʽֵΪ��������ɵ�a2=0����1-2a��0���ٽ⼴�ɣ�
��2�����ݷ�ʽ������������ɵ�1-2a=0���ٽⷽ�̼��ɣ�
��3�����ݷ�ʽֵΪ���ɵ÷��ӷ�ĸΪͬ�ţ����1-2a>0����a��0���ٽⲻ��ʽ���ɣ�
��4�����ݷ�ʽֵΪ���ɵ÷��ӷ�ĸΪ��ţ����1-2a<0����a��0���ٽⲻ��ʽ���ɣ�
��������
(1)������ã�a2=0����1?2a��0��
��ã�... ��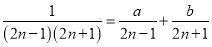 ����������Ȼ��n����������a=_______��b=____��
����������Ȼ��n����������a=_______��b=____��
 -
����������=,
��2n(a+b)+a-b=1������
��ã�a=��b=-.
-
����������=,
��2n(a+b)+a-b=1������
��ã�a=��b=-.