题目内容
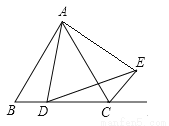
在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图一，若△ABC是等边三角形，且AB=AC=2,点D在线段BC上，
①求证：∠BCE+∠BAC=180°；
②当四边形ADCE的周长取最小值时，求BD的长．
（2）若∠BAC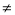
60° ，当点D在射线BC上移动，则∠BCE和∠BAC 之间有怎样的数量关系？并说明理由.
（1）①证明见解析；②BD=2；（2），理由见解析.
【解析】试题分析：
（1）∵
∴
又∵AB=AC，AD=AE
∴△ABD ≌ △ACE
∴
∴
（2）∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
（3）∴
理由如下：
∴ 又∵...
已知：△ABC中，∠B=90°， ∠A、∠C的平分线交于点O，则∠AOC的度数为
A. 60° B. 90° C. 45° D. 135°
D
【解析】
∵∠B=90°，
∴∠BCA+∠BAC=90°，
∵CD平分∠ACB，AE平分∠CAB，
∴∠OCA=∠BCA，∠OAC=∠BAC，
∴∠OCA+∠OAC=∠BCA+∠BAC=（∠BCA+∠BAC）=45°，
∴∠AOC=135°.
故选D. （m-5）2 等于（ ）
A. m2-5 B. m2-5 2 C. m2-10m+25 D. 25m2-5
C
【解析】根据完全平方公式可得：（m-5）2 =m2-10m+25 ，故选C. (c+a2b2)(c-a2b2)等于（ ）
A. c -ab2 B. c2 -a4b4 C. c2 -ab2 D. c2 -a2b2
B
【解析】根据平方差公式可得：(c+a2b2)(c-a2b2)=c2 -a4b4，故选B. （x+6y）（x-6y）等于（ ）
A. x2-6y 2 B. x2-y 2 C. x2-36y 2 D. 36x2-y 2
C
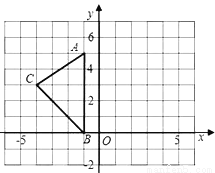
【解析】根据平方差公式可得：（x+6y）（x-6y）=x2-36y 2 ，故选C. 如图，在平面直角坐标系XOY中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）计算△ABC的面积．
（1)画图见解析；（2）7.5
【解析】试题分析：（1）从三角形的各顶点向y轴引垂线并延长相同长度，找对应点．顺次连接即可；（2）根据网格可以看出三角形的底AB是5，高是C到AB的距离，是3，利用面积公式计算．
试题解析：
（1）如图所示：
（2）S△ABC=×5×3= （或7.5）（平方单位）． 用不等式表示“比x的5倍大1的数不小于x的一半”________.
【解析】根据题意可得不等式. 请写出一个同时满足下列条件的分式：
（1）分式的值不可能为0；
（2）分式有意义时，的取值范围是x≠±2；
（3）当x=0时，分式的值为-1.
你所写的分式为 .
（答案不唯一）
【解析】（1）分式的分母不为零、分子不为零；
（2）分式有意义，分母不等于零；
（3）将x=0代入后，分式的分子、分母互为相反数．
【解析】
（1）分式的分子不等于零；
（2）分式有意义时，x的取值范围是x≠±2，即当x=±2时，分式的分母等于零；
（3）当x=0时，分式的值为﹣1，即把x=0代入后，分式的分子、分母互为相反数．
所以满足... 甲、乙两名学生练习计算机打字，甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同．已知甲每分钟比乙每分钟多打5个字，则乙每分钟打______个字．
45
【解析】设乙每分钟打字x个,甲每分钟打个,根据题意可得: ,去分母可得:
,解得,经检验可得: ,故答案为:45.