题目内容
如图,在平面直角坐标系内,四边形OECB的顶点坐标分别是:B(2,5),C(8,5),E(10,0),点P(x,0)是线段OE上一点,设四边形BPEC的面积为S.
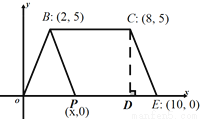
(1)过点C作CD⊥x轴于点E,则CD= , 用含x的代数式表示PE= .
(2)求S与x的函数关系.
(3)当S=30时,直接写出线段PE与PB的长.
 (1)CD=5,PE=10-x;(2)(3)PE=6,PB=
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,P...
(1)CD=5,PE=10-x;(2)(3)PE=6,PB=
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,P...
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )
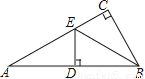
A. 2cm B. 3cm C. 4cm D. 5cm
 B
【解析】试题分析:根据角平分线的性质,由BE平分∠ABC,∠ACB=90°,DE⊥AB,可得CE=DE,即可求得结AE+DE=AE+CE=AC=3cm.
故选B.
B
【解析】试题分析:根据角平分线的性质,由BE平分∠ABC,∠ACB=90°,DE⊥AB,可得CE=DE,即可求得结AE+DE=AE+CE=AC=3cm.
故选B. (3a-b)(3a+b)-(2a-b)(2a+b)
 5a2
【解析】试题分析:先根据平方差公式计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)(2a+b)=9a2-b2-4a2+b2=5a2.
5a2
【解析】试题分析:先根据平方差公式计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)(2a+b)=9a2-b2-4a2+b2=5a2. (2y-3z)(2y+3z)等于( )
A. y2-z2 B. 2y2-3z2 C. 4y2-9z2 D. y2-z2
 C
【解析】根据平方差公式可得:(2y-3z)(2y+3z)=4y2-9z2,故选C.
C
【解析】根据平方差公式可得:(2y-3z)(2y+3z)=4y2-9z2,故选C. (2x+1)(2x-1)等于( )
A. 4x2-1 B. 2x2-1 C. x2-1 D. 2x2+1
 A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A.
A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A. 在所给的8×6网格图中,横竖每相邻两点间的长度均为1,以这些点为顶点的三角形称为网格三角形,请找出点M,使以A,B,M为顶点的网格三角形是直角三角形,这样的点M有_______个.
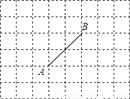
 12
【解析】如图,在线段CD和线段EF上各有5个符合条件的点,图中的两个M点也符合要求,所以符合条件的点M共有12个.
12
【解析】如图,在线段CD和线段EF上各有5个符合条件的点,图中的两个M点也符合要求,所以符合条件的点M共有12个. 函数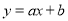 与
与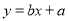 的图象在同一坐标系内的大致( )
的图象在同一坐标系内的大致( )
A. 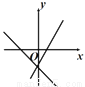 B.
B. 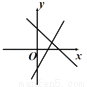 C.
C. 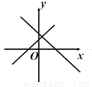 D.
D. 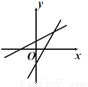
 B
【解析】分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,B选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,B选项符合;④当a<0,b<0时,y=a...
B
【解析】分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,B选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,B选项符合;④当a<0,b<0时,y=a... 若分式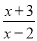 有意义,则
有意义,则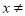 _____.
_____.
 2
【解析】根据分式的分母不等于0时,分式有意义,列出不等式即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故答案为: .
2
【解析】根据分式的分母不等于0时,分式有意义,列出不等式即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故答案为: . 计算: 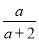 -
-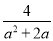 =_____.
=_____.
 【解析】因为-=-=,故答案为: .
【解析】因为-=-=,故答案为: . 
