题目内容
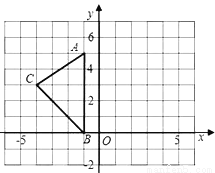
如图，在平面直角坐标系XOY中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）计算△ABC的面积．
（1)画图见解析；（2）7.5
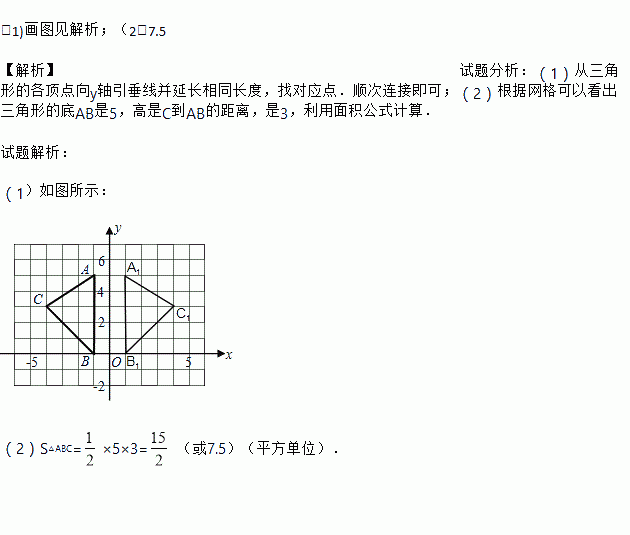
【解析】试题分析：（1）从三角形的各顶点向y轴引垂线并延长相同长度，找对应点．顺次连接即可；（2）根据网格可以看出三角形的底AB是5，高是C到AB的距离，是3，利用面积公式计算．
试题解析：
（1）如图所示：
（2）S△ABC=×5×3= （或7.5）（平方单位）．
练习册系列答案
相关题目
如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB＝6cm，则△DEB的周长为（ ）
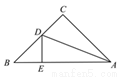
A. 4cm B. 6cm C. 10cm D. 不能确定
B
【解析】∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴DC=DE，
在Rt△AED和Rt△ACD中，
,
∴Rt△AED≌Rt△ACD（HL），
∴AC=AE，
∵AC=BC，
∴∠B=∠CAB=45°，
∴DE=BE，
设DE=BE=x，则DC=x，AE=AC=6－x，
∴BD=x，
∵AC=BC，
∴6－x=... （a-b）（a+b）-（a2+b2）
-2b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
（a-b）（a+b）-（a2+b2）=a2-b2-a2-b2=-2b2. 下面计算正确的是（ ）
A. (a+b)(a-b)=2a+2b B. b5 + b5 = b10 C. x5·x5 = x25 D. (y-z)(y+z)=y2-z2
D
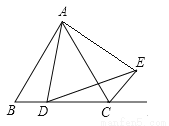
【解析】选项A，原式=a2-b2 ；选项 B，原式=2b5；选项C，原式=x10 ；选项D，原式= y2-z2.故选D. 在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图一，若△ABC是等边三角形，且AB=AC=2,点D在线段BC上，
①求证：∠BCE+∠BAC=180°；
②当四边形ADCE的周长取最小值时，求BD的长．
（2）若∠BAC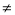
60° ，当点D在射线BC上移动，则∠BCE和∠BAC 之间有怎样的数量关系？并说明理由.
（1）①证明见解析；②BD=2；（2），理由见解析.
【解析】试题分析：
（1）∵
∴
又∵AB=AC，AD=AE
∴△ABD ≌ △ACE
∴
∴
（2）∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
（3）∴
理由如下：
∴ 又∵... 若等腰三角形的一个外角为40°，则它的顶角的度数为_____.
140°
【解析】由等腰三角形的一个外角为40°，可得这个等腰三角形的一个内角为140°，根据三角形的内角和定理可得这个角为等腰三角形的顶角，即这个等腰三角形顶角的度数为140°. 已知图两个中三角形全等，则图2中的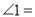
（ ）
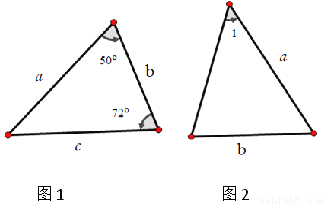
A. 50° B. 58° C. 60° D. 72°
B
【解析】根据三角形的内角和定理求得∠2=180°-50°-72°=58°，根据全等三角形的对应角相等可得∠1=∠2=58°，故选B. 若分式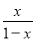
有意义，则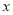
的取值范围是_____.
【解析】根据分式的分母不等于0时，分式有意义，列出不等式即可得出答案.
【解析】
因为分式有意义，
所以，
解得，
故答案为： . 若分式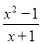
有意义，则x的取值范围为_________．
x≠－1
【解析】由题意得
x+1≠0，
∴x≠-1.