题目内容
如图，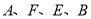 
四点共线， 
， 
， 
， 
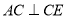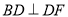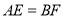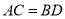.求证：CE∥DF.
证明见解析.
【解析】试题分析：利用HL证明RtΔACE?RtΔBDF，根据全等三角形的性质即可得∠AEC=∠BFD，由内错角相等，两直线平行即可得CE∥DF.
试题解析：
∵AC⊥CE,BD⊥DF，
∴∠ACE=∠BDF=90°，
又∵AE=BF,AC=BD，
∴RtΔACE?RtΔBDF(HL)，
∴∠AEC=∠BFD，
∴CE∥DF.
...
练习册系列答案
相关题目
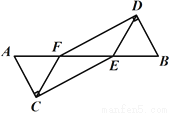
如图，MP⊥NP，MQ为△MNP的角平分线，MT＝MP，连接TQ，则下列结论中不正确的是（ ）
A. TQ＝PQ B. ∠MQT＝∠MQP C. ∠QTN＝90° D. ∠NQT＝∠MQT
D
【解析】∵MQ为△MNP的角平分线，
∴∠PMQ=∠QMT，
∵在△PMQ和△TMQ中，
,
∴△PMQ≌△TMQ，
∴TQ=PQ，∠P=∠QTM=90°，∠MQT＝∠MQP，
故A、B、C选项正确，D选项错误.
故选D. 2（a-b）（a+b）-a2+b2
a2-b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
2（a-b）（a+b）-a2+b2=2a2-2b2-a2+b2=a2-b2. 下面计算错误的是（ ）
A. (y-z)(y+z)=y2-z2 B. (m-n)(m+n)=n2-m C. x5·x20 = x25 D. y3 · y5 = y8
B
【解析】根据平方差公式可得：选项A，(y-z)(y+z)=y2-z2；选项B， (m-n)(m+n)=m2-n2；根据同底数幂的乘法法则可得：选项C，x5·x20 = x25；选项D， y3 · y5 = y8.故选B. 【模型建立】
（1）如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．求证：△BEC≌△CDA；
【模型应用】
（2）如图2，一次函数y=﹣2x+2的图象与y轴交于点A，与x轴交于点B，过点B作线段BC⊥AB且BC=AB，直线AC交x轴于点D．
①求点C的坐标，并直接写出直线AC的函数关系式；
②若点Q是图2中坐标平面内一点，当以点A，D，Q为顶点的三角形是等腰直角三角形时，直接写出点Q的坐标.
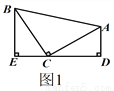
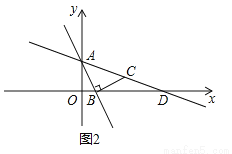
（1）证明见解析；
（2）①；②
【解析】试题分析： 已知直角三角形的直角边分别为5和12，则斜边上的中线为___________．
6.5
【解析】分两种情况：①5和12是两条直角边，根据勾股定理求得斜边为13，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6.5；②5是直角边，12为斜边，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6. 若函数y=(k+1)x+k2-1是正比例函数，则k的值为（ ）
A. 0 B. ﹣1 C. ±1 D. 1
D
【解析】根据正比例函数的定义可得，k2-1=0且k+1≠0，解得k=1，故选D. 若分式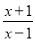
有意义，则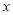
的取值范围是_____．
【解析】根据分式的分母不等于0时，分式有意义，列出不等式即可得出答案.
【解析】
因为分式有意义，
所以，
解得，
故答案为： . 下列分式：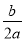 
， 
， 
， 
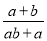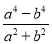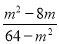，其中最简分式有____个．
2
【解析】因为分式的分子和分母没有公因式,即为最简分式,所以是最简分式, 是最简分式, 的分子和分母中有公因式,所以不是最简分式, 的分子和分母中有公因式,所以不是最简分式,故答案为:2.