如图，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）
A. 1处 B. 2处 C. 3处 D. 4处
D
【解析】如图A、B、C、D为三条直线组成的三角形内角和外角的角平分线的交点，由角平分线上的点到角两边距离相等可得在这四点处，货物中转站到三条公路距离相等.
故选D. 三角形中到三边距离相等的点是（ ）
A. 三条边的中垂线交点 B. 三条高交点
C. 三条中线交点 D. 三条角平分线的交点
D
【解析】由角平分线的性质不难得出三角形中到三边距离相等的点是三条角平分线的交点.
故选D. 如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是（ ）
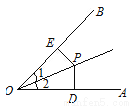
A. PD＝PE B. OD＝OE C. ∠DPO＝∠EPO D. PD＝OP
D
【解析】试题分析：根据角平分线的性质可得：PD=PE，根据题意HL判定定理可得：Rt△POE≌Rt△POD，则OD=OE，∠DPO=∠EPO. 如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB＝6cm，则△DEB的周长为（ ）
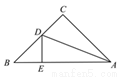
A. 4cm B. 6cm C. 10cm D. 不能确定
B
【解析】∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴DC=DE，
在Rt△AED和Rt△ACD中，
,
∴Rt△AED≌Rt△ACD（HL），
∴AC=AE，
∵AC=BC，
∴∠B=∠CAB=45°，
∴DE=BE，
设DE=BE=x，则DC=x，AE=AC=6－x，
∴BD=x，
∵AC=BC，
∴6－x=... 如图，MP⊥NP，MQ为△MNP的角平分线，MT＝MP，连接TQ，则下列结论中不正确的是（ ）
A. TQ＝PQ B. ∠MQT＝∠MQP C. ∠QTN＝90° D. ∠NQT＝∠MQT
D
【解析】∵MQ为△MNP的角平分线，
∴∠PMQ=∠QMT，
∵在△PMQ和△TMQ中，
,
∴△PMQ≌△TMQ，
∴TQ=PQ，∠P=∠QTM=90°，∠MQT＝∠MQP，
故A、B、C选项正确，D选项错误.
故选D. 如图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3cm，那么AE+DE等于（ ）
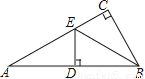
A. 2cm B. 3cm C. 4cm D. 5cm
B
【解析】试题分析：根据角平分线的性质，由BE平分∠ABC，∠ACB=90°，DE⊥AB，可得CE=DE，即可求得结AE+DE=AE+CE=AC=3cm.
故选B. 如图，在Rt△ABC中，∠C=90°，BD是∠ABC的平分线，交AC于点D，若CD=n，AB=m，则△ABD的面积是（ ）
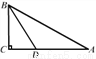
A. mn B.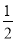 
mn C. 2mn D. 
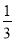mn
B
【解析】
作DE⊥AB交AB于点E，
∵BD是∠ABC的平分线，∠C=90°，
∴CD=DE=n，
∴S△ABD=AB·DE=mn.
故选B. 如图，AB=AD，CB=CD，AC、BD相交于点O，则下列结论正确的是（ ）
A. OA=OC B. 点O到AB、CD的距离相等
C. ∠BDA=∠BDC D. 点O到CB、CD的距离相等
D
【解析】∵在△ADC和△ABC中，
，
∴△ADC≌△ABC，
∴∠DCA=∠BCA，
∴点O到CB、CD的距离相等.
故选D. 已知：△ABC中，∠B=90°， ∠A、∠C的平分线交于点O，则∠AOC的度数为
A. 60° B. 90° C. 45° D. 135°
D
【解析】
∵∠B=90°，
∴∠BCA+∠BAC=90°，
∵CD平分∠ACB，AE平分∠CAB，
∴∠OCA=∠BCA，∠OAC=∠BAC，
∴∠OCA+∠OAC=∠BCA+∠BAC=（∠BCA+∠BAC）=45°，
∴∠AOC=135°.
故选D. 三角形中∠B的平分线和外角的平分线的夹角是（ ）．
A. 60° B. 90° C. 45° D. 135°
B
【解析】
如图，BD平分∠ABF，BE平分∠ABC，
∴∠ABD=∠ABF，∠ABE=∠ABC，
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=（∠ABF+∠ABC）=90°.
故选B.