题目内容
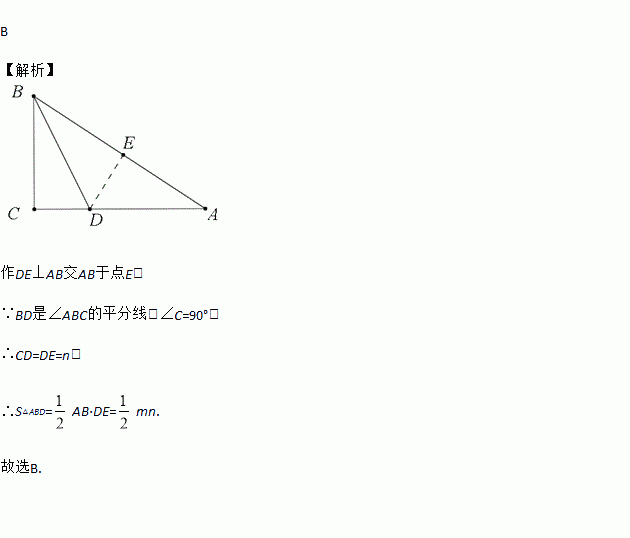
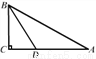
如图，在Rt△ABC中，∠C=90°，BD是∠ABC的平分线，交AC于点D，若CD=n，AB=m，则△ABD的面积是（ ）
A. mn B.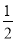 
mn C. 2mn D. 
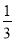mn
B
【解析】
作DE⊥AB交AB于点E，
∵BD是∠ABC的平分线，∠C=90°，
∴CD=DE=n，
∴S△ABD=AB·DE=mn.
故选B.
练习册系列答案
相关题目
分式方程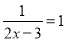
的解为（ ）
A. 2 B. 1 C. -1 D. -2
A
【解析】方程两边都乘2x-3,得
1=2x-3,
解得x-=2.
检验:当x=2时,2x-3≠0.
∴x=2是原方程的解.
所以A选项是正确的. 如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ为底的等腰三角形时，运动的时间是( )秒
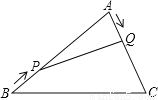
A. 2.5 B. 3 C. 3.5 D. 4
D
【解析】【解析】
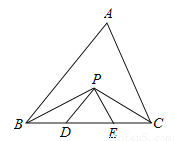
设运动的时间为x，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，当△APQ是等腰三角形时，AP=AQ，AP=20﹣3x，AQ=2x，即20﹣3x=2x，解得x=4．故选D． 如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 cm．
5．
【解析】
试题分析：∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABP=∠PBD，∠ACP=∠PCE，∵PD∥AB，PE∥AC，∴∠ABP=∠BPD，∠ACP=∠CPE，∴∠PBD=∠BPD，∠PCE=∠CPE，∴BD=PD，CE=PE，∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm．故答案为：5． ∠AOB的平分线上一点M ，M到 OA的距离为1.5 cm，则M到OB的距离为_________。
1.5cm
【解析】∵M是∠AOB的平分线上一点，
∴点M到OB的距离等于M到OA的距离，
∴M到OB的距离为1.5cm.
故答案为：1.5cm. 三角形中到三边距离相等的点是（ ）
A. 三条边的中垂线交点 B. 三条高交点
C. 三条中线交点 D. 三条角平分线的交点
D
【解析】由角平分线的性质不难得出三角形中到三边距离相等的点是三条角平分线的交点.
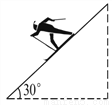
故选D. 某人乘雪橇沿如图所示的斜坡笔直下滑，滑下的距离s(m)与时间t(s)之间的关系式是s＝t2＋10t.若下滑的时间为2s，则此人下滑的高度是_______m.
12
【解析】试题分析：把t＝2代入s＝ t2＋10t中得：
s＝24，
∵三角形是含30°角的直角三角形，
∴此人下滑的高度为：24×＝12米．
故答案为12． [（c2)2+（a2)2]2等于（ ）
A. c8 +2ac4+a8 B. c8 +2a4c+a8 C. c8 +2a4c4+a8 D. c8 +a4c4+a8
C
【解析】根据完全平方公式与幂的乘方法则可得：[（c2)2+（a2)2]2=c8 +2a4c4+a8 ，故选C. 