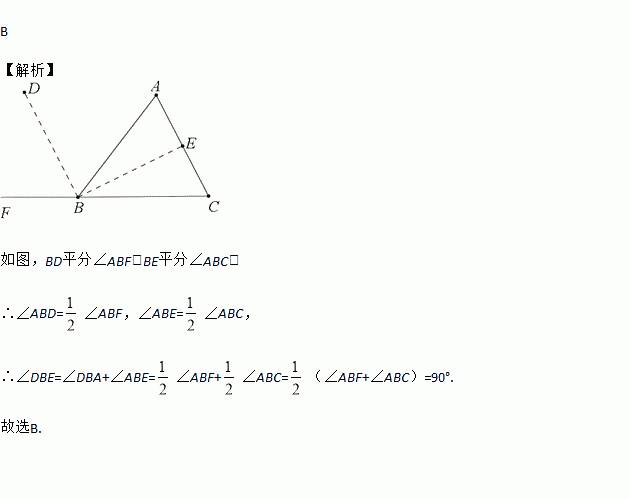题目内容
三角形中∠B的平分线和外角的平分线的夹角是（ ）．
A. 60° B. 90° C. 45° D. 135°
B
【解析】
如图，BD平分∠ABF，BE平分∠ABC，
∴∠ABD=∠ABF，∠ABE=∠ABC，
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=（∠ABF+∠ABC）=90°.
故选B.
练习册系列答案
相关题目
如果关于x的方程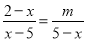
无解，则m等于（ ）
A. 3 B. 4 C. -3 D. 5
A
【解析】去分母，得2－x＝－m，所以x＝2＋m.
若分式方程无解，则x＝2＋m是分式方程的增根，即2＋m＝5，
所以m＝3.
故答案为：3. 等腰三角形周长为36cm，两边长之比为4：1，则底边长为（ ）
A. 16cm B. 4cm C. 20cm D. 16cm或4cm
B
【解析】因为两边长之比为4：1，所以设较短一边为x，则另一边为4x；
(1)假设x为底边，4x为腰；则8x+x=36，x=4，即底边为4；
(2)假设x为腰，4x为底边，则2x+4x=36，x=6，4x=24；
∵6+6＜24，∴该假设不成立．
所以等腰三角形的底边为4cm．
故选B. 如图，AB⊥AC，BF是∠ABC的平分线，若∠BFC=110°，求∠C的度数.
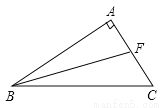
∠C=50°
【解析】试题分析：因为∠BFC=110°，根据三角形的外角等于不相邻的两个内角之和，可以得到∠ABF+∠A=110° ，所以∠ABF=110°－90°=20°，因为BF是∠ABC的角平分线，所以可以得到∠ABC=2∠ABF=40°，即在△ABC中∠C=180°－90°－40°=50°.
试题解析：
∵∠BFC=110°，
∴∠ABF=110°－90°=20°，... 如图，MP⊥NP，MQ为△MNP的角平分线，MT＝MP，连接TQ，则下列结论中不正确的是（ ）
A. TQ＝PQ B. ∠MQT＝∠MQP C. ∠QTN＝90° D. ∠NQT＝∠MQT
D
【解析】∵MQ为△MNP的角平分线，
∴∠PMQ=∠QMT，
∵在△PMQ和△TMQ中，
,
∴△PMQ≌△TMQ，
∴TQ=PQ，∠P=∠QTM=90°，∠MQT＝∠MQP，
故A、B、C选项正确，D选项错误.
故选D. 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是：h＝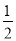
gt2(g表示重力加速度，g取9.8m/s2)．某人发现头顶上空490m处有一炸弹自由下落，其地面杀伤半径为50m，此人发现后，立即以6m/s的速度逃离，那么此人有无危险？
无危险
【解析】试题分析：求出炸弹下落的时间，再算出人在此时间跑出的路程，和50米比较大小即可．
试题解析：
【解析】
无危险，
当h＝490时，490＝×9.8×t2，解得：t＝10秒，
此时人跑的路程为：6×10＝60米＞50米，
所以此人无危险． （5-x2）2等于_______；
25-10x2+x4
【解析】根据完全平方公式可得：（5-x2）2=25-10x2+x4. 
