题目内容
如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )

A. TQ=PQ B. ∠MQT=∠MQP C. ∠QTN=90° D. ∠NQT=∠MQT
 D
【解析】∵MQ为△MNP的角平分线,
∴∠PMQ=∠QMT,
∵在△PMQ和△TMQ中,
,
∴△PMQ≌△TMQ,
∴TQ=PQ,∠P=∠QTM=90°,∠MQT=∠MQP,
故A、B、C选项正确,D选项错误.
故选D.
D
【解析】∵MQ为△MNP的角平分线,
∴∠PMQ=∠QMT,
∵在△PMQ和△TMQ中,
,
∴△PMQ≌△TMQ,
∴TQ=PQ,∠P=∠QTM=90°,∠MQT=∠MQP,
故A、B、C选项正确,D选项错误.
故选D.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知(x-3)2与2|y-2|互为相反数,试求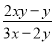 +
+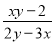 +
+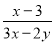 的值.
的值.
 【解析】试题分析:先根据相反数的意义及偶次方和绝对值的非负性,求出x和y的值,然后把所给代数式按照同分母分式的运算法则化简,然后再点入求值.
【解析】
∵(x-3)2与2|y-2|互为相反数,
∴(x-3)2+2|y-2|=0,
∴x-3=0,y-2=0,
∴x=3,y=2,
∴++
=-+
=-
=
=
=
=
【解析】试题分析:先根据相反数的意义及偶次方和绝对值的非负性,求出x和y的值,然后把所给代数式按照同分母分式的运算法则化简,然后再点入求值.
【解析】
∵(x-3)2与2|y-2|互为相反数,
∴(x-3)2+2|y-2|=0,
∴x-3=0,y-2=0,
∴x=3,y=2,
∴++
=-+
=-
=
=
=
= 在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )

A. 4 cm B. 2 cm C. 3 cm D. 1 cm
 C
【解析】∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm.
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm.
故选C.
C
【解析】∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm.
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm.
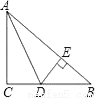
故选C. 如图,△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若DC=7,则点D到AB的距离DE= .
 7
【解析】试题分析: ∵∠C=90°,AD平分∠BAC,点D到AB的距离DE,∴DE=DC=7.故填7.
7
【解析】试题分析: ∵∠C=90°,AD平分∠BAC,点D到AB的距离DE,∴DE=DC=7.故填7. 三角形中∠B的平分线和外角的平分线的夹角是( ).
A. 60° B. 90° C. 45° D. 135°
 B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B.
B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
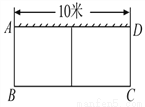
故选B. 如图,有一个长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为45平方米的花圃,那么AB的长为多少米?
 (1)S=-3x2+24x(≤x<8);(2)5米
【解析】试题分析:
(1)可先用x表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
试题解析:
【解析】
(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
这...
(1)S=-3x2+24x(≤x<8);(2)5米
【解析】试题分析:
(1)可先用x表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
试题解析:
【解析】
(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
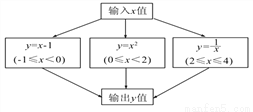
这... 根据下图所示程序计算函数值,若输入的x的值为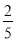 ,则输出的函数值为( )
,则输出的函数值为( )
A. 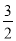 B.
B. 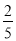 C.
C.  D.
D. 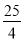
 C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C.
C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C. (c-a2b2)2 等于( )
A. c -ab2 B. c2 -2a2b2c+a4b4 C. c-a2b2c+a4b4 D. c2 -2abc+a4b
 B
【解析】根据完全平方公式可得:(c-a2b2)2=c2 -2a2b2c+a4b4 ,故选B.
B
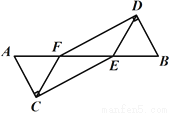
【解析】根据完全平方公式可得:(c-a2b2)2=c2 -2a2b2c+a4b4 ,故选B. 如图, 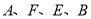 四点共线,
四点共线, 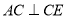 ,
, 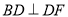 ,
, 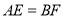 ,
, 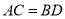 .求证:CE∥DF.
.求证:CE∥DF.
 证明见解析.
【解析】试题分析:利用HL证明RtΔACE?RtΔBDF,根据全等三角形的性质即可得∠AEC=∠BFD,由内错角相等,两直线平行即可得CE∥DF.
试题解析:
∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°,
又∵AE=BF,AC=BD,
∴RtΔACE?RtΔBDF(HL),
∴∠AEC=∠BFD,
∴CE∥DF.
...
证明见解析.
【解析】试题分析:利用HL证明RtΔACE?RtΔBDF,根据全等三角形的性质即可得∠AEC=∠BFD,由内错角相等,两直线平行即可得CE∥DF.
试题解析:
∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°,
又∵AE=BF,AC=BD,
∴RtΔACE?RtΔBDF(HL),
∴∠AEC=∠BFD,
∴CE∥DF.
... 
