题目内容
如图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3cm，那么AE+DE等于（ ）
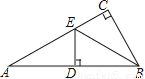
A. 2cm B. 3cm C. 4cm D. 5cm
B
【解析】试题分析：根据角平分线的性质，由BE平分∠ABC，∠ACB=90°，DE⊥AB，可得CE=DE，即可求得结AE+DE=AE+CE=AC=3cm.
故选B.
练习册系列答案
阅读快车系列答案
相关题目
已知A＝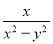
，B＝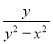
.
(1)计算：A＋B和A－B；
(2)若已知A＋B＝2，A－B＝－1，求x、y的值．
（1）；（2）
【解析】试题分析：（1）将A与B代入A+B与A-B中计算即可得到结果；
（2）根据A+B=2，A-B=-1列出方程组，即可求出x与y的值．
【解析】
(1) ∵A＝，B＝，
∴A＋B＝+＝；
A－B＝-＝＝；
(2)∵A＋B＝2，∴ ＝2，∴x＋y＝，
∵A－B＝－1，∴ ＝－1，∴x－y＝－1，
∴，
∴. 如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是
A. 2 B. 3 C. 4 D. 5
B
【解析】试题分析：如图，AB的垂直平分线与直线y=x相交于点C1，
∵A（0，3），B（0，6），
∴AB=6-3=3，
以点A为圆心，以AB的长为半径画弧，与直线y=x的交点为C2，C3，
∵OB=6，
∴点B到直线y=x的距离为6×，
∵＞3，
∴以点B为圆心，以AB的长为半径画弧，与直线y=x没有交点，
AB的垂直平分线与直线的交点有... 到三角形三边距离相等的点叫做三角形的_________
内心
【解析】到三角形三边距离相等的点为三角形三条角平分线的交点，叫做三角形的内心.
故答案为内心. 到一个角的两边距离相等的点都在_________。
这个角的平分线上
【解析】根据定义可知：到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。 如图，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）
A. 1处 B. 2处 C. 3处 D. 4处
D
【解析】如图A、B、C、D为三条直线组成的三角形内角和外角的角平分线的交点，由角平分线上的点到角两边距离相等可得在这四点处，货物中转站到三条公路距离相等.
故选D. 某校九(1)班共有x名学生，在毕业典礼上每两名同学都握一次手，共握手y次，试写出y与x之间的函数关系式_____________，它______(填“是”或“不是”)二次函数．
y＝x2－ 是
【解析】试题分析：设有x人参加聚会，每个人需要和另外的（x－1）个人握手，所以共握手x(x?1) 次，所以y＝x(x?1)＝x2－，是二次函数．
故答案为：y＝x2－，是． [c-（a2)2]2等于（ ）
A. c -a2 B. c2 -2a4c+a8 C. c2 -a2 D. c2 -a4
B
【解析】根据完全平方公式与幂的乘方法则可得：[c-（a2)2]2=c2 -2a4c+a8 ，故选B. 如图，在平面直角坐标系内，四边形OECB的顶点坐标分别是：B（2，5），C（8，5），E（10，0），点P（x，0）是线段OE上一点，设四边形BPEC的面积为S．
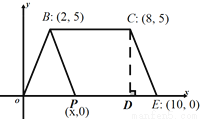
（1）过点C作CD⊥x轴于点E，则CD= ， 用含x的代数式表示PE= .
（2）求S与x的函数关系．
（3）当S＝30时，直接写出线段PE与PB的长．
（1）CD=5，PE=10-x；（2）（3）PE=6，PB=
【解析】试题分析：（1）根据点D的坐标直接求得CD的长，根据点E的坐标表示出PE的长即可；（2）根据已知条件可知四边形BPEC是梯形，利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值，即可求得PE的长，过点B作BM⊥X轴于点M，在Rt△BPM中，根据勾股定理求得PB的长即可.
试题解析：
（1）CD=5，P...