��Ŀ����
��ͼ����ABC�У���C��90�㣬AC��BC��ADƽ�֡�CAB��BC��D��DE��AB��E����AB��6cm�����DEB���ܳ�Ϊ��������
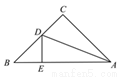
A. 4cm B. 6cm C. 10cm D. ����ȷ��
 B
����������ADƽ�֡�CAB����C=90�㣬DE��AB��
��DC=DE��
��Rt��AED��Rt��ACD��
,
��Rt��AED��Rt��ACD��HL����
��AC=AE��
��AC=BC��
���B=��CAB=45�㣬
��DE=BE��
��DE=BE=x����DC=x��AE=AC=6��x��
��BD=x��
��AC=BC��
��6��x=...
B
����������ADƽ�֡�CAB����C=90�㣬DE��AB��
��DC=DE��
��Rt��AED��Rt��ACD��
,
��Rt��AED��Rt��ACD��HL����
��AC=AE��
��AC=BC��
���B=��CAB=45�㣬
��DE=BE��
��DE=BE=x����DC=x��AE=AC=6��x��
��BD=x��
��AC=BC��
��6��x=...
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д��Ȼ�������ֵ��(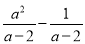 )��
)��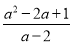 ������a��3.
������a��3.
 2
��������������������⿼���˷�ʽ�Ļ�����ֵ���Ȱ������ﰴ��ͬ��ĸ��ʽ�ļӼ�������Ȼ��ѳ���ת��Ϊ�˷������ѷ��ӷ�ĸ�ֽ���ʽԼ�֣���������ֵ����.
��������
()��
=��
=��
=��
=��
��a��3ʱ��
ԭʽ===2.
2
��������������������⿼���˷�ʽ�Ļ�����ֵ���Ȱ������ﰴ��ͬ��ĸ��ʽ�ļӼ�������Ȼ��ѳ���ת��Ϊ�˷������ѷ��ӷ�ĸ�ֽ���ʽԼ�֣���������ֵ����.
��������
()��
=��
=��
=��
=��
��a��3ʱ��
ԭʽ===2. �ڵ�����ABC�У�AB=AC�����ܳ�Ϊ20cm����AB�ߵ�ȡֵ��Χ�ǣ� ��
A. 1cm��AB��4cm B. 5cm��AB��10cm
C. 4cm��AB��8cm D. 4cm��AB��10cm
 B
��������������������ڵ�����ABC�У�AB=AC�����ܳ�Ϊ20cm������AB="AC=x" cm����BC=��20��2x��cm���࣬���5cm��x��10cm����ѡB��
B
��������������������ڵ�����ABC�У�AB=AC�����ܳ�Ϊ20cm������AB="AC=x" cm����BC=��20��2x��cm���࣬���5cm��x��10cm����ѡB�� �ڡ�ABC�У���C=90�㣬ADƽ�֡�BAC��BC��D����BC=32����BD��CD=9��7����D��AB�ľ���Ϊ______
 18
���������������������D��DE��AB����BC=32��BD��CD=9��7���������CD�ij����ٸ��ݽ�ƽ���ߵ����ʼ�����ý��.
����D��DE��AB��
��BD��CD=9��7��
��CD=BC��=14
��ADƽ�֡�CAB��DE��AB����C=90��
��DE=CD=14
18
���������������������D��DE��AB����BC=32��BD��CD=9��7���������CD�ij����ٸ��ݽ�ƽ���ߵ����ʼ�����ý��.
����D��DE��AB��
��BD��CD=9��7��
��CD=BC��=14
��ADƽ�֡�CAB��DE��AB����C=90��
��DE=CD=14 ��֪����ABC�У���B=90�㣬 ��A����C��ƽ���߽��ڵ�O�����AOC�Ķ���Ϊ
A. 60�� B. 90�� C. 45�� D. 135��
 D
��������
�ߡ�B=90�㣬
���BCA+��BAC=90�㣬
��CDƽ�֡�ACB��AEƽ�֡�CAB��
���OCA=��BCA����OAC=��BAC��
���OCA+��OAC=��BCA+��BAC=����BCA+��BAC��=45�㣬
���AOC=135��.
��ѡD.
D
��������
�ߡ�B=90�㣬
���BCA+��BAC=90�㣬
��CDƽ�֡�ACB��AEƽ�֡�CAB��
���OCA=��BCA����OAC=��BAC��
���OCA+��OAC=��BCA+��BAC=����BCA+��BAC��=45�㣬
���AOC=135��.
��ѡD. ij���й���һ�ֵ���Ϊ40Ԫ����������Ե���50Ԫ���ۣ���ôÿ�¿��۳�500�����������۾��飬�ۼ�ÿ���1Ԫ����������Ӧ����10����������н������ۼ۶�ΪxԪ(x��50)��ÿ�����������������yԪ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)���мƻ��������������������8000Ԫ����Ҫ��������Ĺ˿ͣ���ô����������ۼ�Ӧ��Ϊ����Ԫ��
 (1) y����10x2��1400x��40000��50��x��100����2��60Ԫ.
�������������������1���������������������ϵ�������ۼۣ����۾Ϳ��Եó�ÿ������������������������������ΪyԪ���������������������ϵ��ʾ��y��x֮��ĺ�����ϵʽ��
��2�����ֵy��8000����ú��ʵ�x��ֵ���ɣ�
���������
��������
��1�������⣬�����ۼ۶�ΪxԪ����ÿ����������...
(1) y����10x2��1400x��40000��50��x��100����2��60Ԫ.
�������������������1���������������������ϵ�������ۼۣ����۾Ϳ��Եó�ÿ������������������������������ΪyԪ���������������������ϵ��ʾ��y��x֮��ĺ�����ϵʽ��
��2�����ֵy��8000����ú��ʵ�x��ֵ���ɣ�
���������
��������
��1�������⣬�����ۼ۶�ΪxԪ����ÿ����������... �ڰ뾶Ϊ4cm ��Բ�У���ȥһ���뾶Ϊxcm ��Բ�棬ʣ��һ��Բ�������Ϊycm2����y��x�ĺ�����ϵʽΪ( )
A.y=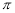 x2-4 B.y=
x2-4 B.y=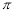 (2-x)2 C.y=-(x2+4) D.y=-
(2-x)2 C.y=-(x2+4) D.y=-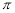 x2+16
x2+16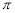
 D
��������
����������������ô�Բ�������ȥСԲ��������ɵõ����.
�������y��x�ĺ�����ϵʽΪy=-x2+16����ѡD.
D
��������
����������������ô�Բ�������ȥСԲ��������ɵõ����.
�������y��x�ĺ�����ϵʽΪy=-x2+16����ѡD. (x+3ab)2 ���ڣ� ��
A. x2+6xab+9a2b2 B. x2+6ab+9a2b2 C. x2+xab+9a2b2 D. x2+6xab+a2b2
 A
��������������ȫƽ����ʽ�ɵã�(x+3ab)2 =x2+6xab+9a2b2����ѡA.
A
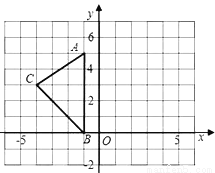
��������������ȫƽ����ʽ�ɵã�(x+3ab)2 =x2+6xab+9a2b2����ѡA. ��ͼ����ƽ��ֱ������ϵXOY�У�A����1��5����B����1��0����C����4��3����
��1���뻭����ABC����y��ԳƵġ�A��B��C�䣨����A�䣬B�䣬C��ֱ���A��B��C�Ķ�Ӧ�㣬��д��������
��2�������ABC�������
 ��1)��ͼ����������2��7.5
�������������������1���������εĸ�������y�������߲��ӳ���ͬ���ȣ��Ҷ�Ӧ�㣮˳�����Ӽ��ɣ���2������������Կ��������εĵ�AB��5������C��AB�ľ��룬��3�����������ʽ���㣮
���������
��1����ͼ��ʾ��
��2��S��ABC=��5��3= ����7.5����ƽ����λ����
��1)��ͼ����������2��7.5
�������������������1���������εĸ�������y�������߲��ӳ���ͬ���ȣ��Ҷ�Ӧ�㣮˳�����Ӽ��ɣ���2������������Կ��������εĵ�AB��5������C��AB�ľ��룬��3�����������ʽ���㣮
���������
��1����ͼ��ʾ��
��2��S��ABC=��5��3= ����7.5����ƽ����λ���� 
