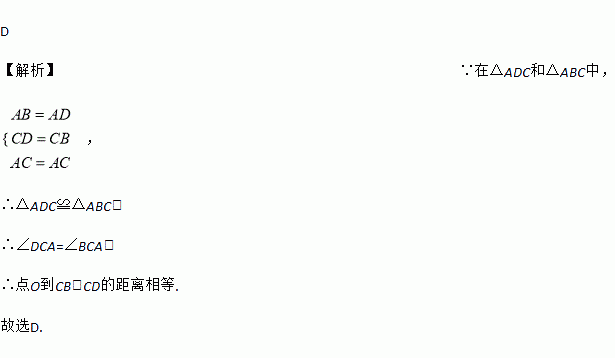题目内容
如图，AB=AD，CB=CD，AC、BD相交于点O，则下列结论正确的是（ ）
A. OA=OC B. 点O到AB、CD的距离相等
C. ∠BDA=∠BDC D. 点O到CB、CD的距离相等
D
【解析】∵在△ADC和△ABC中，
，
∴△ADC≌△ABC，
∴∠DCA=∠BCA，
∴点O到CB、CD的距离相等.
故选D.
练习册系列答案
一线名师提优试卷系列答案
相关题目
若分式方程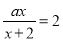
的解为2，则a的值为（ ）
A. 4 B. 1 C. 0 D. 2
A
【解析】根据分式方程的解的定义把x=2代入分式方程得到关于a的方程，解出即可。
把x=2代入分式方程得 ，解得a=4，故选A. 等腰但不等边的三角形的角平分线、高线、的总条数是（ ）
A．3 B．5 C．7 D．9
C．
【解析】
试题分析：等腰但不等边的三角形底边上的角平分线、中线、高线三线重合成一条；腰上的三条线不重合，因而共有7条线．
故选C． 已知：AC=AD,AB是∠CAD的角平分线，求证：BC=BD.
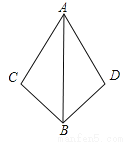
证明见解析.
【解析】证明：∵AB是∠CAD的角平分线
∴∠BAC=∠BAD ……………………………………………1分
在△ABC和△ABD中
……………………………………3分
∴△ABC≌△ABD …………………………4分
∴BC=BD 如图，∠AOB=60°，PD⊥OA于D，PE⊥OB于E，且PD=PE，则∠1=________
30°
【解析】由角平分逆定理可知：∠1=∠2=30°.
故的答案为30°. 如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是（ ）
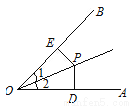
A. PD＝PE B. OD＝OE C. ∠DPO＝∠EPO D. PD＝OP
D
【解析】试题分析：根据角平分线的性质可得：PD=PE，根据题意HL判定定理可得：Rt△POE≌Rt△POD，则OD=OE，∠DPO=∠EPO. 函数y＝(m＋2)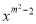 
＋2x－1(x≠0)，当m＝___时，它是二次函数，当m＝_________时，它为一次函数．
2， ±或－2
【解析】试题分析：令m2－2＝2，得m＝2或－2，
∵m＋2≠0，m≠－2，
∴m＝2，
即m＝2时是二次函数；
当m＝－2时，y＝2x－1，是一次函数，
当m2－2＝1，即m＝时， 是一次函数，
即m＝或－2时， 是一次函数．
故答案为2； 或－2． （c+a)2等于（ ）
A. c3 -a3 B. a2+2ac+c2 C. c5 -a5 D. c2 -2ac+a2
B
【解析】根据完全平方公式可得：（c+a)2=a2+2ac+c2，故选B.