等腰三角形的对称轴是______．
顶角平分线所在直线
【解析】一个图形沿一条直线对折，直线两旁的部分能够完全重合，那么这个图形就是轴对称图形，这条直线就是这个图形的一条对称轴,如图所示：等腰三角形的对称轴是顶角平分线所在直线.
故答案是：顶角平分线所在直线. △ABC中，AB=AC，∠A=36°，BD平分∠ABC，则∠1 =_______度，此三角形有_______个等腰三角形．
72° 3
【解析】∵AB=AC，∠A=36°，
∴△ABC是等腰三角形，∠C=∠ABC=（180°?36°）=72°.
∵BD为∠ABC的平分线，
∴∠ABD=∠A=∠DBC=36°，
∴AD=BD，△ADB是等腰三角形，
∴∠1=180°-36°-72°=72°=∠C，
∴BC=BD，△CDB是等腰三角形.
图中共有3个等腰三角形． 在△ABC中，与∠A相邻的外角是100°，要使△ABC是等腰三角形，则∠B的度是_________.
80°或50°或20°
【解析】∵∠A的相邻外角是100°，∴∠A=80°．
分两种情况：
（1）当∠A为底角时，另一底角∠B=∠A=80°；
（2）当∠A为顶角时，则底角∠B=∠C= (180°?80°) =50°
（3）当∠B是顶角时，∠B=180°-2∠A=20°．
综上所述，∠B的度数是80°或50°或20°. △ABC中，若∠A=80°，∠B=50°，AC=5，则AB= ．
5.
【解析】
试题解析：∵∠A=80°，∠B=50°，
∴∠C=180°-80°-50°=50°，
∴AB=AC=5． 在△ABC中，AB=AC，AD是BC边上的高，∠C=63°，BC=4，求∠BAD的度数及DC的长.
27° 2
【解析】试题分析：根据等腰三角形的两个底角相等求出顶角∠BAC的度数，再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°，DC=BC=2.
试题解析：
∵AB=AC，∠C=63°，
∴∠B=∠C=63°，
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高，
∴AD是∠BAC的平分线，AD是BC边上的中线，
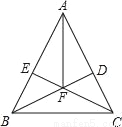
... 如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
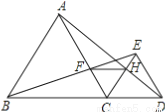
∴... 如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形.BE交AC于F，AD交CE于H，求证：
（1）△BCE≌△ACD；
（2）CF=CH；
（3）△FCH是等边三角形；
（4）FH∥BD.
见解析
【解析】试题分析：（1）由等边三角形的三边相等，三角都是60°，再根据平角的关系，就能证明△BCE≌△ACD；（2）由△BCE≌△ACD得出对应角相等，结合等边三角形的边角特点证明△BCF≌△ACH，能得出CF=CH；（3）两边等，加上一个角60°推出△CFH是等边三角形；（4）根据内错角相等，两直线平行推出FH∥BD.
试题解析：
证明：∵△ABC和△CDE都是等边三角... 如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．
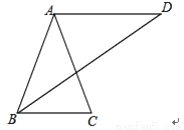
证明见解析.
【解析】试题分析：首先根据AB=AC=AD，可得∠C=∠ABC，∠D=∠ABD，∠ABC=∠CBD+∠D；然后根据AD∥BC，可得∠CBD=∠D，据此判断出∠ABC=2∠D，再根据∠C=∠ABC，即可判断出∠C=2∠D．
试题解析：∵AB=AC=AD，
∴∠C=∠ABC，∠D=∠ABD.
∴∠ABC=∠CBD＋∠D.
∵AD∥BC，
∴∠CBD=∠... 如图，在△ABC 中，∠B 与∠C 的平分线交于点O， 过O 点作DE ∥BC，分别交AB、AC于D、E，若AB=5，AC=4，求△ADE 的周长.
9
【解析】试题分析：由在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，易证得△DOB与△EOC是等腰三角形，即DO=DB，EO=EC，继而可得△ADE的周长等于AB+AC，即可求得答案．
试题解析：
∵在△ABC中，∠B与∠C的平分线交于点O，
∴∠DBO=∠CBO，∠ECO=∠BCO，
∵DE∥BC，
∴∠DOB=∠CBO，∠EOC=∠BCO，... 计算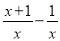
的结果为( )
A. 1 B. x C.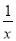 
D. 
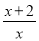
A
【解析】试题解析：原式
故选A.