题目内容
如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．
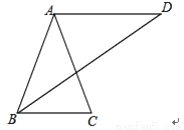
证明见解析.
【解析】试题分析：首先根据AB=AC=AD，可得∠C=∠ABC，∠D=∠ABD，∠ABC=∠CBD+∠D；然后根据AD∥BC，可得∠CBD=∠D，据此判断出∠ABC=2∠D，再根据∠C=∠ABC，即可判断出∠C=2∠D．
试题解析：∵AB=AC=AD，
∴∠C=∠ABC，∠D=∠ABD.
∴∠ABC=∠CBD＋∠D.
∵AD∥BC，
∴∠CBD=∠...
练习册系列答案
一本好题口算题卡系列答案
相关题目
如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件_________使四边形AECF是平行四边形(只填一个即可).
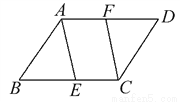
AF=CE（答案不唯一）
【解析】试题分析：添加的条件是AF=CE．理由是：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴AF∥CE，
∵AF=CE，
∴四边形AECF是平行四边形． 分式方程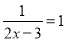
的解为（ ）
A. 2 B. 1 C. -1 D. -2
A
【解析】方程两边都乘2x-3,得
1=2x-3,
解得x-=2.
检验:当x=2时,2x-3≠0.
∴x=2是原方程的解.
所以A选项是正确的. 计算：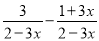 
1
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式 计算：
= ．
x．
【解析】
试题分析：===x．故答案为：x． 在△ABC中，与∠A相邻的外角是100°，要使△ABC是等腰三角形，则∠B的度是_________.
80°或50°或20°
【解析】∵∠A的相邻外角是100°，∴∠A=80°．
分两种情况：
（1）当∠A为底角时，另一底角∠B=∠A=80°；
（2）当∠A为顶角时，则底角∠B=∠C= (180°?80°) =50°
（3）当∠B是顶角时，∠B=180°-2∠A=20°．
综上所述，∠B的度数是80°或50°或20°. 如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ为底的等腰三角形时，运动的时间是( )秒
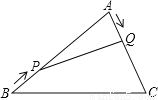
A. 2.5 B. 3 C. 3.5 D. 4
D
【解析】【解析】
设运动的时间为x，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，当△APQ是等腰三角形时，AP=AQ，AP=20﹣3x，AQ=2x，即20﹣3x=2x，解得x=4．故选D． 如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 cm．
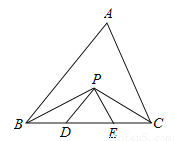
5．
【解析】
试题分析：∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABP=∠PBD，∠ACP=∠PCE，∵PD∥AB，PE∥AC，∴∠ABP=∠BPD，∠ACP=∠CPE，∴∠PBD=∠BPD，∠PCE=∠CPE，∴BD=PD，CE=PE，∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm．故答案为：5． [（c2)2+（a2)2]2等于（ ）
A. c8 +2ac4+a8 B. c8 +2a4c+a8 C. c8 +2a4c4+a8 D. c8 +a4c4+a8
C
【解析】根据完全平方公式与幂的乘方法则可得：[（c2)2+（a2)2]2=c8 +2a4c4+a8 ，故选C.