题目内容
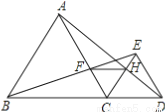
如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形.BE交AC于F，AD交CE于H，求证：
（1）△BCE≌△ACD；
（2）CF=CH；
（3）△FCH是等边三角形；
（4）FH∥BD.
见解析
【解析】试题分析：（1）由等边三角形的三边相等，三角都是60°，再根据平角的关系，就能证明△BCE≌△ACD；（2）由△BCE≌△ACD得出对应角相等，结合等边三角形的边角特点证明△BCF≌△ACH，能得出CF=CH；（3）两边等，加上一个角60°推出△CFH是等边三角形；（4）根据内错角相等，两直线平行推出FH∥BD.
试题解析：
证明：∵△ABC和△CDE都是等边三角...
练习册系列答案
导学教程高中新课标系列答案
相关题目
如图所示，在□ABCD中，AC与BD相交于点O，AB⊥AC，∠DAC＝45°，AC＝2，则BD的长是_______．
2
【解析】∵四边形ABCD是平行四边形，∠DAC=45°，
∴∠ACB=∠DAC=45°，OA=AC=1，
∵AB⊥AC，
∴△ABC是等腰直角三角形，
∴AB=AC=2，
在Rt△AOB中，根据勾股定理得OB= ，
∴BD=2BO=2. 已知A＝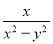
，B＝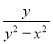
.
(1)计算：A＋B和A－B；
(2)若已知A＋B＝2，A－B＝－1，求x、y的值．
（1）；（2）
【解析】试题分析：（1）将A与B代入A+B与A-B中计算即可得到结果；
（2）根据A+B=2，A-B=-1列出方程组，即可求出x与y的值．
【解析】
(1) ∵A＝，B＝，
∴A＋B＝+＝；
A－B＝-＝＝；
(2)∵A＋B＝2，∴ ＝2，∴x＋y＝，
∵A－B＝－1，∴ ＝－1，∴x－y＝－1，
∴，
∴. 计算：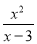 
-
x＋3
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式 下列各式计算正确的是( )
A.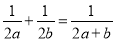 
B. 
C. 
D. 
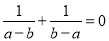
D
【解析】试题解析：A.原式故A错误；
B.原式故B错误；
C.原式故C错误；
D.正确.
故选D. △ABC中，AB=AC，∠A=36°，BD平分∠ABC，则∠1 =_______度，此三角形有_______个等腰三角形．
72° 3
【解析】∵AB=AC，∠A=36°，
∴△ABC是等腰三角形，∠C=∠ABC=（180°?36°）=72°.
∵BD为∠ABC的平分线，
∴∠ABD=∠A=∠DBC=36°，
∴AD=BD，△ADB是等腰三角形，
∴∠1=180°-36°-72°=72°=∠C，
∴BC=BD，△CDB是等腰三角形.
图中共有3个等腰三角形． 如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是
A. 2 B. 3 C. 4 D. 5
B
【解析】试题分析：如图，AB的垂直平分线与直线y=x相交于点C1，
∵A（0，3），B（0，6），
∴AB=6-3=3，
以点A为圆心，以AB的长为半径画弧，与直线y=x的交点为C2，C3，
∵OB=6，
∴点B到直线y=x的距离为6×，
∵＞3，
∴以点B为圆心，以AB的长为半径画弧，与直线y=x没有交点，
AB的垂直平分线与直线的交点有... 到三角形三边距离相等的点叫做三角形的_________
内心
【解析】到三角形三边距离相等的点为三角形三条角平分线的交点，叫做三角形的内心.
故答案为内心. [c-（a2)2]2等于（ ）
A. c -a2 B. c2 -2a4c+a8 C. c2 -a2 D. c2 -a4
B
【解析】根据完全平方公式与幂的乘方法则可得：[c-（a2)2]2=c2 -2a4c+a8 ，故选B.