题目内容
计算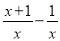
的结果为( )
A. 1 B. x C.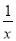 
D. 
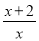
A
【解析】试题解析：原式
故选A.
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
一个多边形的内角和与外角和相加正好是一个九边形的内角和，试求这个多边形的边数.
7
【解析】试题分析：设这个多边形的边数为n,根据多边形内角和与外角和定理得出(n－2) ×180º+360º=(9－2)×180º，,解之可得.
【解析】
设这个多边形的边数为n，则根据题意，
得 (n－2)·180º+360º=(9－2)×180º，
解得n=7.
所以这个多边形的边数为7. .分式方程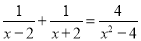
的解是（ ）
A. 无解 B. x=2 C. x=-2 D. x=2或x=-2
A
【解析】去分母得：x+2+x-2=4，2x=4,
解得：x=2，
检验:当x=2时,(x-2)(x+2)=0.所以原方程无解.
故选A. 计算：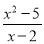 
-
-
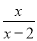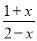
x＋2
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式 计算：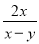 
＋
＝__
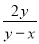2
【解析】试题解析：原式
故答案为：2. 在△ABC中，AB=AC，AD是BC边上的高，∠C=63°，BC=4，求∠BAD的度数及DC的长.
27° 2
【解析】试题分析：根据等腰三角形的两个底角相等求出顶角∠BAC的度数，再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°，DC=BC=2.
试题解析：
∵AB=AC，∠C=63°，
∴∠B=∠C=63°，
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高，
∴AD是∠BAC的平分线，AD是BC边上的中线，
... 已知△ABC中，三边a，b，c满足|b-c|+（a-b）2=0，则∠A等于（ ）
A. 60° B. 45° C. 90° D. 不能确定
A
【解析】△ABC中，三边a，b，c满足|b-c|+（a-b）2=0∴b-c=0，a-b=0，
∴a=b=c，
∴a=b=c，
∴三角形是等边三角形，
∴∠A=60°.
故选A. 在△ABC中，AB=BC，∠ABC=84°，BD是∠ABC的平分线，DE∥BC；求∠EDB的度数.
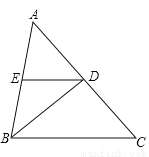
∠EDB=42°.
【解析】试题分析：因为BD是∠ABC的平分线，所以∠ABD=∠CBD，所以∠DBC=84°÷2=42°，因为DE∥BC，所以∠EDB=∠DBC=42°.
试题解析：
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD，
∴∠DBC=84°÷2=42°，
∵DE∥BC，
∴∠EDB=∠DBC=42°. （d+f）2等于（ ）
A. d3 -f3 B. d2 +2df+f 2 C. d2 -2f+f 2 D. d2 -df+f 2
B
【解析】根据完全平方公式可得：（d+f）2=d2 +2df+f 2，故选B.