阅读下面题目的计算过程：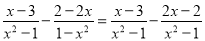 
①
＝x－3－2x＋2②
＝－x－1.③
(1)上面计算过程从哪一步开始出现错误？请写出该步骤的代号__；
(2)错误原因是__________；
(3)本题的正确结论是________.
② 丢了分母 －
【解析】∵
∴从第②步开始出错;错误原因是:丢了分母;正确结论是: －. 计算：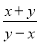 
+
-
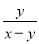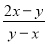
1
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式 计算：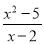 
-
-
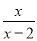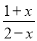
x＋2
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式 先化简，再求值：(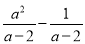
)÷
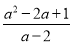，其中a＝3.
2
【解析】试题分析：本题考查了分式的化简求值，先把括号里按照同分母分式的加减法化简，然后把除法转化为乘法，并把分子分母分解因式约分，最后代入求值即可.
【解析】
()÷
=÷
=×
=×
=，
当a＝3时，
原式===2. 已知(x－3)2与2|y－2|互为相反数，试求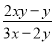
＋
＋
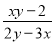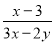的值．
【解析】试题分析：先根据相反数的意义及偶次方和绝对值的非负性，求出x和y的值，然后把所给代数式按照同分母分式的运算法则化简，然后再点入求值.
【解析】
∵(x－3)2与2|y－2|互为相反数，
∴(x－3)2+2|y－2|=0，
∴x-3=0，y-2=0,
∴x=3，y=2,
∴＋＋
=-＋
=-
=
=
=
= 已知A＝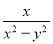
，B＝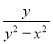
.
(1)计算：A＋B和A－B；
(2)若已知A＋B＝2，A－B＝－1，求x、y的值．
（1）；（2）
【解析】试题分析：（1）将A与B代入A+B与A-B中计算即可得到结果；
（2）根据A+B=2，A-B=-1列出方程组，即可求出x与y的值．
【解析】
(1) ∵A＝，B＝，
∴A＋B＝+＝；
A－B＝-＝＝；
(2)∵A＋B＝2，∴ ＝2，∴x＋y＝，
∵A－B＝－1，∴ ＝－1，∴x－y＝－1，
∴，
∴. 分式方程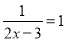
的解为（ ）
A. 2 B. 1 C. -1 D. -2
A
【解析】方程两边都乘2x-3,得
1=2x-3,
解得x-=2.
检验:当x=2时,2x-3≠0.
∴x=2是原方程的解.
所以A选项是正确的. 若分式方程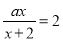
的解为2，则a的值为（ ）
A. 4 B. 1 C. 0 D. 2
A
【解析】根据分式方程的解的定义把x=2代入分式方程得到关于a的方程，解出即可。
把x=2代入分式方程得 ，解得a=4，故选A. .分式方程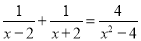
的解是（ ）
A. 无解 B. x=2 C. x=-2 D. x=2或x=-2
A
【解析】去分母得：x+2+x-2=4，2x=4,
解得：x=2，
检验:当x=2时,(x-2)(x+2)=0.所以原方程无解.
故选A. 如果关于x的方程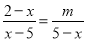
无解，则m等于（ ）
A. 3 B. 4 C. -3 D. 5
A
【解析】去分母，得2－x＝－m，所以x＝2＋m.
若分式方程无解，则x＝2＋m是分式方程的增根，即2＋m＝5，
所以m＝3.
故答案为：3.