题目内容
先化简,再求值:(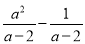 )÷
)÷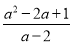 ,其中a=3.
,其中a=3.
 2
【解析】试题分析:本题考查了分式的化简求值,先把括号里按照同分母分式的加减法化简,然后把除法转化为乘法,并把分子分母分解因式约分,最后代入求值即可.
【解析】
()÷
=÷
=×
=×
=,
当a=3时,
原式===2.
2
【解析】试题分析:本题考查了分式的化简求值,先把括号里按照同分母分式的加减法化简,然后把除法转化为乘法,并把分子分母分解因式约分,最后代入求值即可.
【解析】
()÷
=÷
=×
=×
=,
当a=3时,
原式===2.
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
下列变形错误的是( )
A. 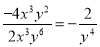 B.
B. 
C.  D.
D. 
 D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D.
D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D. 在□ABCD中,∠B=100°,则∠A,∠D的度数分别是( )
A. ∠A=80°,∠D=80° B. ∠A=80°,∠D=100°
C. ∠A=100°,∠D=80° D. ∠A=100°,∠D=100°
 B
【解析】∵在□ABCD中,∠B=100°,
∴∠A=180°-∠B=180°-100°=80°, ∠D=∠B=100°.
故选B.
B
【解析】∵在□ABCD中,∠B=100°,
∴∠A=180°-∠B=180°-100°=80°, ∠D=∠B=100°.
故选B. 下列各式变形正确的是( )
A. 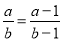 B.
B. 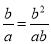 C.
C. 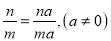 D.
D. 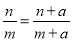
 C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。
C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。 .分式方程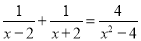 的解是( )
的解是( )
A. 无解 B. x=2 C. x=-2 D. x=2或x=-2
 A
【解析】去分母得:x+2+x-2=4,2x=4,
解得:x=2,
检验:当x=2时,(x-2)(x+2)=0.所以原方程无解.
故选A.
A
【解析】去分母得:x+2+x-2=4,2x=4,
解得:x=2,
检验:当x=2时,(x-2)(x+2)=0.所以原方程无解.
故选A. 化简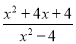 -
-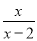 =______.
=______.
 【解析】-
=-
=-
=
【解析】-
=-
=-
= 计算: 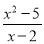 -
-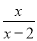 -
-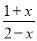
 x+2
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式
x+2
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式 在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.
 27° 2
【解析】试题分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°,DC=BC=2.
试题解析:
∵AB=AC,∠C=63°,
∴∠B=∠C=63°,
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高,
∴AD是∠BAC的平分线,AD是BC边上的中线,
...
27° 2
【解析】试题分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°,DC=BC=2.
试题解析:
∵AB=AC,∠C=63°,
∴∠B=∠C=63°,
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高,
∴AD是∠BAC的平分线,AD是BC边上的中线,
... 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为( )
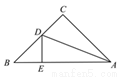
A. 4cm B. 6cm C. 10cm D. 不能确定
 B
【解析】∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE,
在Rt△AED和Rt△ACD中,
,
∴Rt△AED≌Rt△ACD(HL),
∴AC=AE,
∵AC=BC,
∴∠B=∠CAB=45°,
∴DE=BE,
设DE=BE=x,则DC=x,AE=AC=6-x,
∴BD=x,
∵AC=BC,
∴6-x=...
B
【解析】∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE,
在Rt△AED和Rt△ACD中,
,
∴Rt△AED≌Rt△ACD(HL),
∴AC=AE,
∵AC=BC,
∴∠B=∠CAB=45°,
∴DE=BE,
设DE=BE=x,则DC=x,AE=AC=6-x,
∴BD=x,
∵AC=BC,
∴6-x=... 
