若分式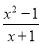 有意义,则x的取值范围为_________.
有意义,则x的取值范围为_________.
 x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1.
x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1. 对于分式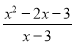 ,当x=__时,分式无意义;当x=__时,分式值为零.
,当x=__时,分式无意义;当x=__时,分式值为零.
 3, -1
【解析】当x-3=0时,分式无意义,
解之得
x=3;
当 时,分式值为零,
解之得
x=-1.
3, -1
【解析】当x-3=0时,分式无意义,
解之得
x=3;
当 时,分式值为零,
解之得
x=-1. 填空:  =1÷(____),
=1÷(____),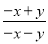 =﹣(____) ÷(x+y).
=﹣(____) ÷(x+y).
 x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y).
x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y). 下列各式① ;②
;②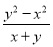 ;③
;③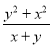 ;④
;④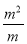 ;⑤
;⑤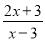 中分子与分母没有公因式的分式是__.(填序号)
中分子与分母没有公因式的分式是__.(填序号)
 ③⑤
【解析】①∵=, ∴分子与分母有公因式3;
②∵∴分子与分母有公因式x+y;
③的分子与分母没有公因式;
④∵∴分子与分母有公因式m;
⑤的分子与分母没有公因式.
∴③和⑤的分子与分母没有公因式.
③⑤
【解析】①∵=, ∴分子与分母有公因式3;
②∵∴分子与分母有公因式x+y;
③的分子与分母没有公因式;
④∵∴分子与分母有公因式m;
⑤的分子与分母没有公因式.
∴③和⑤的分子与分母没有公因式. 若关于x的方程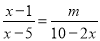 无解,则m=___________.
无解,则m=___________.
 -8 .
【解析】试题分析:去分母可得:x-1=-,解得:x=1-,根据分式无解可知x=5,即1-=5,解得:m=-8.
-8 .
【解析】试题分析:去分母可得:x-1=-,解得:x=1-,根据分式无解可知x=5,即1-=5,解得:m=-8. 在方程 中,如果设y=x2﹣4x,那么原方程可化为关于y的整式方程是__.
中,如果设y=x2﹣4x,那么原方程可化为关于y的整式方程是__.
 【解析】方程可变形为x2-4x++4=0,因为,所以,整理得,
【解析】方程可变形为x2-4x++4=0,因为,所以,整理得, 若 ,对任意自然数n都成立,则a=_______,b=____.
,对任意自然数n都成立,则a=_______,b=____.
 -
【解析】∵=,
∴2n(a+b)+a-b=1,即,
解得:a=,b=-.
-
【解析】∵=,
∴2n(a+b)+a-b=1,即,
解得:a=,b=-. 当y=x+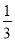 时,
时,  的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3. 计算:
(1) (2)
(2) ÷(4x2﹣y2)
÷(4x2﹣y2)
 (1) ;(2)
【解析】试题分析:(1)考查了分式的乘除混合运算,从左到右依次计算即可;(2)先把除法转化为乘法,然后把分子和分母分解因式约分.
【解析】
(1)原式=×
=;
(2)原式=•
=(2x﹣y)•
=;
(1) ;(2)
【解析】试题分析:(1)考查了分式的乘除混合运算,从左到右依次计算即可;(2)先把除法转化为乘法,然后把分子和分母分解因式约分.
【解析】
(1)原式=×
=;
(2)原式=•
=(2x﹣y)•
=; 解下列方程:
(1)1﹣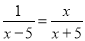 (2)
(2)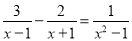 .
.
 (1) ;(2)x=-5
【解析】试题分析:先去分母,把分式方程转化为整式方程,然后按照整式方程的解法求解,求出未知数的值后要验根.
【解析】
(1)去分母得:x2﹣25﹣x﹣5=x2﹣5x,
解得:x=,
经检验x=是分式方程的解;
(2)去分母得:3x+3﹣2x+3=1,
解得:x=﹣5,
经检验x=﹣5是分式方程的解.
(1) ;(2)x=-5
【解析】试题分析:先去分母,把分式方程转化为整式方程,然后按照整式方程的解法求解,求出未知数的值后要验根.
【解析】
(1)去分母得:x2﹣25﹣x﹣5=x2﹣5x,
解得:x=,
经检验x=是分式方程的解;
(2)去分母得:3x+3﹣2x+3=1,
解得:x=﹣5,
经检验x=﹣5是分式方程的解.