题目内容
若分式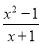
有意义，则x的取值范围为_________．
x≠－1
【解析】由题意得
x+1≠0，
∴x≠-1.
练习册系列答案
相关题目
甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000千克，乙每次用去800元，而不管购买多少饲料.
（1）甲、乙所购饲料的平均单价各是多少？
（2）谁的购货方式更合算？
（1）甲的平均单价为元/千克，乙平均单价为元/千克；（2）乙的购货方式更合算.
【解析】【试题分析】（1）设第一次饲料的价格为x元/千克，第二次饲料的价格为y元/千克，根据平均价格= ，代入即可.则这两次所购饲料的平均单价元/千克.则甲的平均单价为 元/千克；乙所购的饲料的平均单价为 元/千克.
(2)利用作差法比较大小即可.得： ，由于 ，得乙的购货方式更合算.
【试题解析... 已知|a-4|+
，计算
·
的值.
【解析】试题分析：利用非负数的性质，可求得a、b的值，然后将分式化简，进而可代值求解．
试题解析：
∴a?4=0且b?9=0，
∴a=4，b=9.
原式
当a=4,b=9时,原式 已知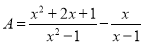
.
（1）化简A；
（2）当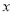
满足不等式组
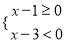，且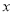
为整数时，求A的值.
（1）；（2）1
【解析】试题分析：首先将分式的分子和分母进行因式分解，然后进行约分，最后根据同分母的分式减法法则得出化简的答案；根据题意求出不等式组的整数解，然后根据分式的性质求出x的值，将x的值代入化简后的式子进行计算.
试题解析：（1）原式====
（2）不等式组的解集为1≤x＜3 ∵x为整数 ∴x=1或2
∵A=∴x－1≠0 即x≠1 ∴x=2
当x=2时，原... 在方程
中，如果设y=x2﹣4x，那么原方程可化为关于y的整式方程是__．
【解析】方程可变形为x2-4x++4=0,因为，所以，整理得， 使分式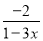
的值为正的条件是（ ）
A.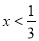 
B.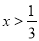 
C. x＜0 D. x＞0
B
【解析】由题意得
1-3x<0,
解之得
.
故选B. 如图，在平行四边形ABCD中，AB=4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG=1，则AE的边长为（ ）.
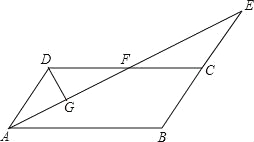
A．2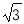
B．4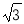
C．4 D．8
B.
【解析】
试题分析：由AE为角平分线，得到一对角相等，再由ABCD为平行四边形，得到AD与BE平行，利用两直线平行内错角相等得到一对角相等，等量代换及等角对等边得到AD=DF，由F为DC中点，AB=CD，求出AD与DF的长，得出三角形ADF为等腰三角形，根据三线合一得到G为AF中点，在直角三角形ADG中，由AD与DG的长，利用勾股定理求出AG的长，进而求出AF的长，再由三角形AD... 一个多边形的内角和与外角和的度数之比为2∶1，则这个多边形的边数为（ ）
A. 3 B. 4 C. 5 D. 6
D
【解析】设这个多边形有n条边，由题意得
(n-2) ×180:360=2:1,
解之得
n=6.
故选D. 计算：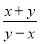 
+
-
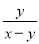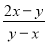
1
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式