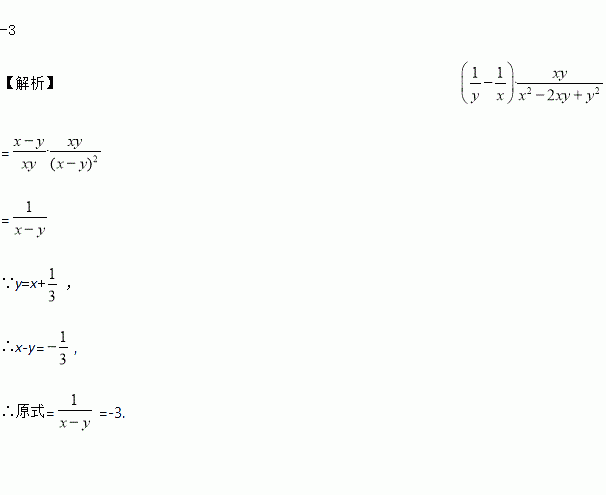题目内容
当y=x+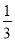 时,
时,  的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
练习册系列答案
相关题目
在多边形的内角中,锐角的个数不能多于( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B.
B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B. 若对于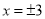 以外的一切数
以外的一切数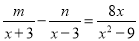 均成立,则
均成立,则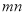 的值是( )
的值是( )
A. 8 B. 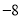 C. 16 D.
C. 16 D. 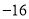
 D
【解析】,则 ,得: .
故选D.
D
【解析】,则 ,得: .
故选D. 化简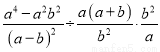 的结果是( )
的结果是( )
A. 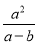 B.
B. 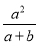 C.
C. 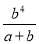 D.
D. 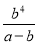
 D
【解析】试题解析:原式
故选D.
D
【解析】试题解析:原式
故选D. 已知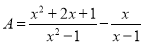 .
.
(1)化简A;
(2)当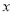 满足不等式组
满足不等式组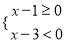 ,且
,且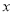 为整数时,求A的值.
为整数时,求A的值.
 (1);(2)1
【解析】试题分析:首先将分式的分子和分母进行因式分解,然后进行约分,最后根据同分母的分式减法法则得出化简的答案;根据题意求出不等式组的整数解,然后根据分式的性质求出x的值,将x的值代入化简后的式子进行计算.
试题解析:(1)原式====
(2)不等式组的解集为1≤x<3 ∵x为整数 ∴x=1或2
∵A=∴x-1≠0 即x≠1 ∴x=2
当x=2时,原...
(1);(2)1
【解析】试题分析:首先将分式的分子和分母进行因式分解,然后进行约分,最后根据同分母的分式减法法则得出化简的答案;根据题意求出不等式组的整数解,然后根据分式的性质求出x的值,将x的值代入化简后的式子进行计算.
试题解析:(1)原式====
(2)不等式组的解集为1≤x<3 ∵x为整数 ∴x=1或2
∵A=∴x-1≠0 即x≠1 ∴x=2
当x=2时,原... 填空:  =1÷(____),
=1÷(____),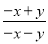 =﹣(____) ÷(x+y).
=﹣(____) ÷(x+y).
 x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y).
x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y). 使分式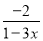 的值为正的条件是( )
的值为正的条件是( )
A. 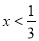 B.
B. 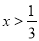 C. x<0 D. x>0
C. x<0 D. x>0
 B
【解析】由题意得
1-3x<0,
解之得
.
故选B.
B
【解析】由题意得
1-3x<0,
解之得
.
故选B. 如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
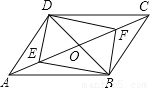
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B. (2016内蒙古包头市)化简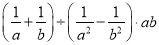 ,其结果是( )
,其结果是( )
A. 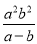 B.
B. 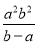 C.
C. 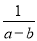 D.
D. 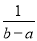
 B
【解析】= .
所以选B.
B
【解析】= .
所以选B.