若关于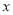 的方程
的方程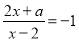 的解为正数,则
的解为正数,则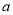 的取值范围是_____.
的取值范围是_____.
 且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且.
且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且. 若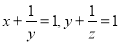 ,则
,则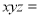 _____.
_____.
 -1
【解析】根据得: .
故答案:-1.
-1
【解析】根据得: .
故答案:-1. 设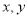 是两个不同的正整数,且
是两个不同的正整数,且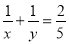 ,则
,则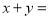 _____.
_____.
 18
【解析】根据,得:5(x+y)=2xy,
因为x、y都是整数,则 ,则
18
【解析】根据,得:5(x+y)=2xy,
因为x、y都是整数,则 ,则 为改善环境,张村拟在荒山上种植960棵树,由于共青团员的支持,每日比原计划多种20棵,结果提前4天完成任务,原计划每天种植多少棵?设原计划每天种植x棵,根据题意得方程______________.
 【解析】设原计划每天种植x棵,根据题意:
故答案: .
【解析】设原计划每天种植x棵,根据题意:
故答案: . 观察下列各式: 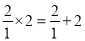 ,
, 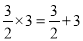 ;
; 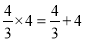 ;
; 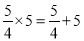 ;…想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为________________.
;…想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为________________.
 【解析】根据一系列的等式,发现:满足 的两个数的积等于它们的和(n表示正整数). 用关于n的等式表示这个规律为.
故答案: .
【解析】根据一系列的等式,发现:满足 的两个数的积等于它们的和(n表示正整数). 用关于n的等式表示这个规律为.
故答案: . 解分式方程:
(1)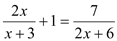
(2)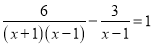
 (1) (2)x=-4
【解析】【试题分析】(1)方程两边同时乘以 ,则 ;移项及合并得: 系数化为1: .经检验: 是原方程的根.
(2)方程两边同时乘以 ,去分母得: 去括号得: 移项得: 解得: 经检验,x=-4是原方程的根.
【试题解析】
方程两边同时乘以 ,则 ;
移项及合并得:
系数化为1: .
经检验: 是原方程的根.
方程两边同时乘以...
(1) (2)x=-4
【解析】【试题分析】(1)方程两边同时乘以 ,则 ;移项及合并得: 系数化为1: .经检验: 是原方程的根.
(2)方程两边同时乘以 ,去分母得: 去括号得: 移项得: 解得: 经检验,x=-4是原方程的根.
【试题解析】
方程两边同时乘以 ,则 ;
移项及合并得:
系数化为1: .
经检验: 是原方程的根.
方程两边同时乘以... 已知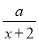 与
与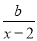 的和等于
的和等于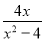 ,求
,求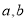 之值.
之值.
 a=2,b=2
【解析】【试题分析】根据题意得: 变形 ,得: 得: ,从而得解.
【试题解析】
根据题意,有
+=.
去分母,得
.
去括号,整理得
.
比较两边多项式系数,得
.
解得.
a=2,b=2
【解析】【试题分析】根据题意得: 变形 ,得: 得: ,从而得解.
【试题解析】
根据题意,有
+=.
去分母,得
.
去括号,整理得
.
比较两边多项式系数,得
.
解得. 解方程:
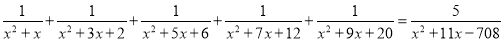 .
.
 x=118
【解析】【试题分析】用拆项法解方程, = 将方程左边化简为= ,再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根.
x=118
【解析】【试题分析】用拆项法解方程, = 将方程左边化简为= ,再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根. 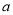 为何值时,分式方程
为何值时,分式方程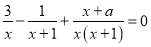 无解?
无解?
 当或时原分式方程无解
【解析】【试题分析】方程的两边同乘以,去分母,得:
整理,得.
即,把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;当 时, ,
于是当或时原分式方程无解.
【试题解析】
方程的两边同乘以,去分母,得
整理,得。
即.
把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;
...
当或时原分式方程无解
【解析】【试题分析】方程的两边同乘以,去分母,得:
整理,得.
即,把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;当 时, ,
于是当或时原分式方程无解.
【试题解析】
方程的两边同乘以,去分母,得
整理,得。
即.
把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;
... 某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
 (1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程,有:
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,...
(1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程,有:
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,...