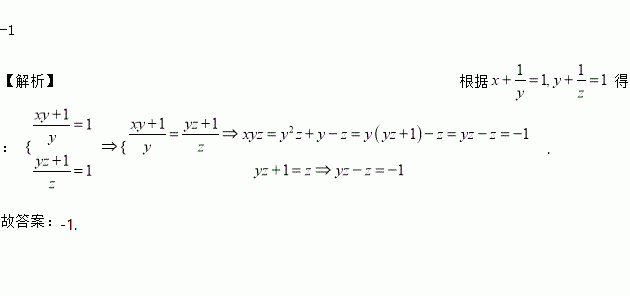题目内容
若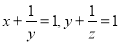 ,则
,则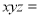 _____.
_____.
 -1
【解析】根据得: .
故答案:-1.
-1
【解析】根据得: .
故答案:-1.
练习册系列答案
相关题目
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).
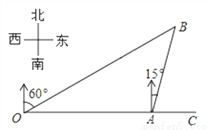
 【解析】试题分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=km.
【解析】
如图,过点A作AD⊥OB于D.
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB?∠AOB=75...
【解析】试题分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=km.
【解析】
如图,过点A作AD⊥OB于D.
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB?∠AOB=75... 正十边形的每个外角为________
 36°
【解析】正十边形的一个外角为:360°÷10=36°,
故答案为:36°.
36°
【解析】正十边形的一个外角为:360°÷10=36°,
故答案为:36°. 如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A. 6 B. 9 C. 14 D. 20
 B
【解析】设多边形的边数为n,则有:(n-2)•180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
故选B.
B
【解析】设多边形的边数为n,则有:(n-2)•180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
故选B. 已知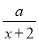 与
与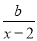 的和等于
的和等于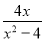 ,求
,求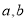 之值.
之值.
 a=2,b=2
【解析】【试题分析】根据题意得: 变形 ,得: 得: ,从而得解.
【试题解析】
根据题意,有
+=.
去分母,得
.
去括号,整理得
.
比较两边多项式系数,得
.
解得.
a=2,b=2
【解析】【试题分析】根据题意得: 变形 ,得: 得: ,从而得解.
【试题解析】
根据题意,有
+=.
去分母,得
.
去括号,整理得
.
比较两边多项式系数,得
.
解得. 已知x-y=4xy,则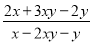 的值为________.
的值为________.
 【解析】因为 则= .
故答案:
【解析】因为 则= .
故答案: 分式方程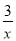 +
+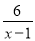 =
=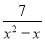 的解为x=____________.
的解为x=____________.
 【解析】+=,去分母得: 移项及合并得: 系数化为1得: .
故答案: .
【解析】+=,去分母得: 移项及合并得: 系数化为1得: .
故答案: . 求下列各式的值.
(1)已知xa=2,xb=6,x≠0,求x3a-2b的值;
(2)若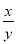 = -2,求
= -2,求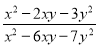 的值.
的值.
 (1) ;(2) .
【解析】试题分析: 根据同底数幂的除法和幂的乘方进行运算即可.
将进行变形,代入所求式子进行运算即可.
试题解析:
原式
(1) ;(2) .
【解析】试题分析: 根据同底数幂的除法和幂的乘方进行运算即可.
将进行变形,代入所求式子进行运算即可.
试题解析:
原式 如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF. 求证:四边形BECF是平行四边形.
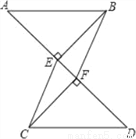
 见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)...
见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)...