题目内容
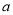 为何值时,分式方程
为何值时,分式方程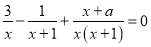 无解?
无解?
 当或时原分式方程无解
【解析】【试题分析】方程的两边同乘以,去分母,得:
整理,得.
即,把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;当 时, ,
于是当或时原分式方程无解.
【试题解析】
方程的两边同乘以,去分母,得
整理,得。
即.
把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;
...
当或时原分式方程无解
【解析】【试题分析】方程的两边同乘以,去分母,得:
整理,得.
即,把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;当 时, ,
于是当或时原分式方程无解.
【试题解析】
方程的两边同乘以,去分母,得
整理,得。
即.
把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;
...
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
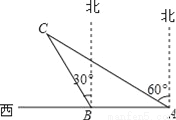
如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: 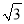 ≈1.732)
≈1.732)
 17.
【解析】试题分析:过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
试题解析:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴...
17.
【解析】试题分析:过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
试题解析:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴... 如图,在?ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
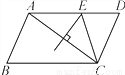
A. 7 B. 10 C. 11 D. 12
 B
【解析】试题分析:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
【解析】
∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
...
B
【解析】试题分析:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
【解析】
∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
... 四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数为( )
A. 80° B. 90° C. 170° D. 20°
 A
【解析】试题分析:四边形的内角和为360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°,
故选A.
A
【解析】试题分析:四边形的内角和为360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°,
故选A. 如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A. 6 B. 9 C. 14 D. 20
 B
【解析】设多边形的边数为n,则有:(n-2)•180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
故选B.
B
【解析】设多边形的边数为n,则有:(n-2)•180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
故选B. 为改善环境,张村拟在荒山上种植960棵树,由于共青团员的支持,每日比原计划多种20棵,结果提前4天完成任务,原计划每天种植多少棵?设原计划每天种植x棵,根据题意得方程______________.
 【解析】设原计划每天种植x棵,根据题意:
故答案: .
【解析】设原计划每天种植x棵,根据题意:
故答案: . 已知x-y=4xy,则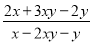 的值为________.
的值为________.
 【解析】因为 则= .
故答案:
【解析】因为 则= .
故答案: 设轮船在静水中的速度为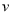 ,该船在流水(速度为
,该船在流水(速度为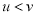 )中从上游A驶往下游B,再返回A,所用的时间为T,假设
)中从上游A驶往下游B,再返回A,所用的时间为T,假设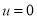 ,即河流改为静水,该船从A至B再返回A,所用时间为
,即河流改为静水,该船从A至B再返回A,所用时间为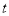 ,则( )
,则( )
A. 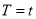 B.
B. 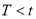 C.
C. 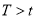 D. 不能确定T与
D. 不能确定T与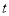 的大小关系
的大小关系
 C
【解析】设AB=s,则 故选C.
C
【解析】设AB=s,则 故选C. 若x=-1,y=2,则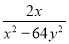 -
-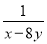 的值为( )
的值为( )
A. -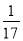 B.
B. 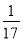 C.
C. 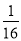 D.
D. 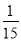
 D
【解析】试题分析:原式====,
当, 时,原式==.故选D.
D
【解析】试题分析:原式====,
当, 时,原式==.故选D. 
