题目内容
某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
 (1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程,有:
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,...
(1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程,有:
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,...
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
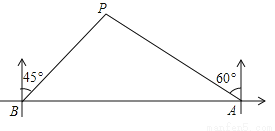
 小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里
【解析】试题分析:过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、AM、BP.
试题解析:如图:过P作PM⊥AB于M,则∠PMB=∠PMA=90°,∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20,∴PM=AP=10,AM=PM=,∴∠BPM=...
小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里
【解析】试题分析:过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、AM、BP.
试题解析:如图:过P作PM⊥AB于M,则∠PMB=∠PMA=90°,∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20,∴PM=AP=10,AM=PM=,∴∠BPM=... 如图,?ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
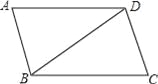
A. 16° B. 22° C. 32° D. 68°
 C
【解析】试题分析:根据平行四边形的性质可知:AD∥BC,所以∠C+∠ADC=180°,再由BC=BD可得∠C=∠BDC=74°,进而可求出∠ADB=106°﹣74°=32°.
故选:C.
C
【解析】试题分析:根据平行四边形的性质可知:AD∥BC,所以∠C+∠ADC=180°,再由BC=BD可得∠C=∠BDC=74°,进而可求出∠ADB=106°﹣74°=32°.
故选:C. 内角和等于外角和2倍的多边形是( )
A. 五边形 B. 六边形 C. 七边形 D. 八边形
 B
【解析】试题分析:本题应先设这个多边形的边数为n,则依题意可列出方程(n﹣2)×180°=360°×2,从而解出n=6,即这个多边形的边数为6.
【解析】
设这个多边形的边数为n,则依题意可得:
(n﹣2)×180°=360°×2,
解得n=6,
∴这个多边形的边数为6.
故选B.
B
【解析】试题分析:本题应先设这个多边形的边数为n,则依题意可列出方程(n﹣2)×180°=360°×2,从而解出n=6,即这个多边形的边数为6.
【解析】
设这个多边形的边数为n,则依题意可得:
(n﹣2)×180°=360°×2,
解得n=6,
∴这个多边形的边数为6.
故选B. 一个多边形中,除一个内角外,其余各内角和是120°,则这个角的度数是( )
A. 60° B. 80° C. 100° D. 120°
 A
【解析】根据多边形的内角和公式可以知道,多边形的内角和是180°的正整数倍,所以只有A选项和120°相加是180°的正整数倍,
故选A.
A
【解析】根据多边形的内角和公式可以知道,多边形的内角和是180°的正整数倍,所以只有A选项和120°相加是180°的正整数倍,
故选A. 观察下列各式: 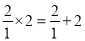 ,
, 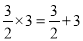 ;
; 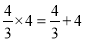 ;
; 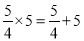 ;…想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为________________.
;…想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为________________.
 【解析】根据一系列的等式,发现:满足 的两个数的积等于它们的和(n表示正整数). 用关于n的等式表示这个规律为.
故答案: .
【解析】根据一系列的等式,发现:满足 的两个数的积等于它们的和(n表示正整数). 用关于n的等式表示这个规律为.
故答案: . 已知: 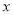 满足方程
满足方程 ,则代数式
,则代数式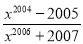 的值是_____.
的值是_____.
 【解析】因为,则 .
故答案: .
【解析】因为,则 .
故答案: . 下列各式从左到右的变形正确的是( )
A.  B.
B. 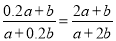
C. 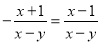 D.
D. 
 A
【解析】选项A:分子分母同时乘以2得到答案,正确;
选项B: ==,所以错误;
选项C: ==,所以错误;
选项D: ==,所以错误.
故选:A.
A
【解析】选项A:分子分母同时乘以2得到答案,正确;
选项B: ==,所以错误;
选项C: ==,所以错误;
选项D: ==,所以错误.
故选:A. 关于x的分式方程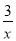 +
+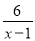 -
-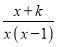 =0有解,则k满足( )
=0有解,则k满足( )
A. k≠-3 B. k≠5
C. k≠-3且k≠-5 D. k≠-3且k≠5
 D
【解析】原分式方程去分母,得
3(x-1)+6x=x+k,
整理,得
8x-k-3=0,
解得
x=,
要使分式方程不会产生增根,则x≠0且x≠1,
∴≠0且≠1.
解得,k≠-3且k≠5
故选D.
D
【解析】原分式方程去分母,得
3(x-1)+6x=x+k,
整理,得
8x-k-3=0,
解得
x=,
要使分式方程不会产生增根,则x≠0且x≠1,
∴≠0且≠1.
解得,k≠-3且k≠5
故选D. 
