小明乘滑草车沿坡比为1：2.4的斜坡下滑130米，求他下降的高度
50米
【解析】试题分析：根据坡比可设BC=x，AC=2.4x，根据勾股定理得出AB=2.6x，根据AB的长度得出x的值，从而得出BC的值，即下降的高度．
试题解析：∵坡比为1：2.4， ∴BC：AC=1：2.4， 设BC=x，AC=2.4x，
则AB= ∵AB=130米， ∴x=50， 则BC=x=50（米）． 抛物线y＝2(x－3)2＋1的顶点坐标是( )
A. (3，1) B. (3，－1) C. (－3，1) D. (－3，－1)
A
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y＝2(x－3)2＋1的顶点坐标是（3，1）．
故选：A． 若二次函数y＝x2＋bx＋4配方后为y＝(x－2)2＋k，则b、k的值分别为( )
A. 0，5 B. 0，1 C. －4，5 D. －4，0
D
【解析】∵二次函数y＝x2＋bx＋4配方后是y＝（x－2）2＋k
∴a=1， -=2， c=4
∴b=-4
∴ k==1
故选：D. 抛物线y＝x2＋bx＋c的图象先向右平移2个单位，再向下平移3个单位，所得图象的函数解析式为y＝(x－1)2－4，则b，c的值分别为( )
A. b＝2，c＝－6 B. b＝2，c＝0
C. b＝－6，c＝8 D. b＝－6，c＝2
B
【解析】试题分析：先确定出平移后的抛物线的顶点坐标，然后根据向右平移横坐标加，向下平移纵坐标减求出平移前的抛物线的顶点坐标，然后写出平移前的抛物线的顶点式形式，然后整理成一般形式，即可得到b、c的值．
【解析】
函数y=（x﹣1）2﹣4的顶点坐标为（1，﹣4），
∵是向右平移2个单位，再向下平移3个单位得到，
∴1﹣2=﹣1，﹣4+3=﹣1，
∴平移前的抛物线的... 已知二次函数y＝－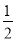
x2－7x＋
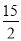，若自变量x分别取x1、x2、x3，且0＜x1＜x2＜x3，则对应的函数值y1、y2、y3的大小关系正确的是( )
A. y1＞y2＞y3 B. y1＜y2＜y3 C. y2＞y3＞y1 D. y2＜y3＜y1
A
【解析】∵二次函数y＝－x2－7x＋，∴此函数的对称轴为：x＝－＝－＝－7.∵0已知抛物线y＝x2－2x＋m＋1与x轴有两个不同的交点，则函数y＝
的大致图象是( )
A. （A） B. （B） C. （C） D. （D）
A
【解析】抛物线y=x2-2x+m+1与x轴有两个不同的交点，可得△=（-2）2-4（m+1）＞0，解得m＜0，因此可得函数y=的图象位于二、四象限，
故选：A． 某市烟花厂为该市4.18烟花三月经贸旅游特别设计制作一种新型礼炮，这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h＝－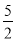
t2＋20t＋1.若这种礼炮点火开空到最高点处引爆，则从点火升空到引爆需要的时间为( )
A. 3s B. 4s C. 5s D. 6s
B
【解析】把二次函数的一般式写成顶点式h=-t2+20t+1=-（t-4）2+41，找出顶点坐标（4，41），当t=4时，升到最高点．
故选：B． 如图，在平面直角坐标系中，抛物线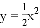
经过平移得到抛物线
，其对称轴与两段抛物线所围成的阴影部分的面积为
A. 2 B. 4 C. 8 D. 16
B
【解析】试题解析：过点C作CA⊥y，
∵抛物线y=x2-2x=（x2-4x）=（x2-4x+4）-2=（x-2）2-2，
∴顶点坐标为C（2，-2），
对称轴与两段抛物线所围成的阴影部分的面积为：2×2=4，
故选B． 已知二次函数y＝ax2＋bx＋c的图象如图，则下列叙述正确的是( )
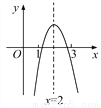
A. abc＜0 B. －3a＋c＜0
C. b2－4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y＝ax2＋c
B
【解析】解：A．由开口向下，可得a＜0；又由抛物线与y轴交于负半轴，可得c＜0，然后由对称轴在y轴右侧，得到b与a异号，则可得b＞0，故得abc＞0，故本选项错误；
B．根据图知对称轴为直线x=2，即=2，得b=﹣4a，再根据图象知当x=1时，y=a+b+c=a﹣4a+c=﹣3a+c＜0，故本选项正确；
C．由抛物线与x轴有两个交点，可得b2﹣4ac＞0，故本选项错误；
... 二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是( )
A. k＜－3 B. k＞－3 C. k＜3 D. k＞3
D
【解析】试题分析：∵当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，
∴此时y=|ax2+bx+c|=ax2+bx+c，
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，
∵当ax2+bx+c＜0时，y=ax2+bx+c（a≠0）的图象在x轴下方，
∴此时y=|ax2+bx+c|=﹣（ax2+b...