题目内容
已知二次函数y＝－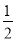
x2－7x＋
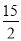，若自变量x分别取x1、x2、x3，且0＜x1＜x2＜x3，则对应的函数值y1、y2、y3的大小关系正确的是( )
A. y1＞y2＞y3 B. y1＜y2＜y3 C. y2＞y3＞y1 D. y2＜y3＜y1
A
【解析】∵二次函数y＝－x2－7x＋，∴此函数的对称轴为：x＝－＝－＝－7.∵0
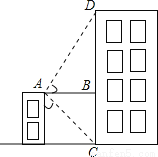
每日10分钟口算心算速算天天练系列答案从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（ ）
A．（6+6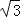
）米 B．（6+3
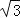）米 C．（6+2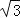）米 D．12米
A
【解析】
试题分析：在Rt△ACB中，∠CAB=45°，AB⊥DC，AB=6，
∴BC=AB=6，
在Rt△ABD中，∵tan∠BAD=，
∴BD=AB•tan∠BAD=6，
∴DC=CB+BD=6+6（m）．
故选A． 函数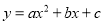
的图象如图所示，则下列结论错误的是（ ）
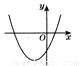
A. a＞0 B. b2－4ac＞0
C.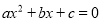 
的两根之和为负 D. 
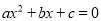的两根之积为正
D
【解析】【解析】
∵抛物线开口向上，∴a＞0，故A正确．
∵抛物线与x轴有两个交点，∴b2－4ac＞0，故B正确．
由图象可知， 一根为正，一根为负，且负根的绝对值大于正根的绝对值，∴两根之和为负，两根之积为负，故C正确，D错误．
故选D． 已知二次函数y＝－x2＋4，当－2≤x≤3时，函数的最小值是_____，最大值是____．
－5 4
【解析】试题解析：抛物线y＝－x2＋4，开口向下，有最大值为4，当x=3时有最小值为-5. 二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是( )
A. k＜－3 B. k＞－3 C. k＜3 D. k＞3
D
【解析】试题分析：∵当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，
∴此时y=|ax2+bx+c|=ax2+bx+c，
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，
∵当ax2+bx+c＜0时，y=ax2+bx+c（a≠0）的图象在x轴下方，
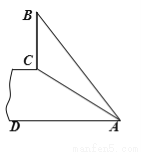
∴此时y=|ax2+bx+c|=﹣（ax2+b... 如图，斜坡AC的坡度（坡比）为1: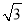 
，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．
6米.
【解析】
试题分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．
试题解析：延长BC交AD于E点，则CE⊥AD．
在Rt△AEC中，AC=10，由坡比为1：可知：∠CAE=30°，
∴... 如图，在坡度为1：3的山坡上种树，要求株距（相邻两树间的水平距离）是6米，则斜坡上相邻两树间的坡面距离是 米（结果保留根号）．
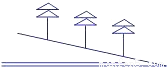
2.
【解析】
试题分析：如图，
Rt△ABC中，∠C=90°，tanA=，AC=6，
∴BC=AC•tanA=6×=2．
根据勾股定理，得：AB=．
即斜坡上相邻两树间的坡面距离是2米． 如图2 - 4所示，长方形ABCD的长为5 cm，宽为4 cm，如果将它的长和宽都减去x(cm)，那么它剩下的小长方形AB′C′D′的面积为y(cm2)．
(1)写出y与x的函数关系式；
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
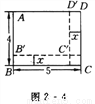
(1) y＝x2－9x＋20；(2) 二次函数;(3) 0＜x＜4.
【解析】试题分析：（1）根据长方形的面积公式，根据图示求解即可得到函数关系式；
（2）通过二次函数的定义可判断；
（3）根据x取值不能大于原方程的长方形的宽进行分析.
试题解析：(1)根据长方形的面积公式，得y＝(5－x)·(4－x)＝x2－9x＋20，所以y与x的函数关系式为y＝x2－9x＋20．
... 下列由左到右的变形中，哪些是分解因式?哪些不是?请说出理由.
（1）a（x+y）=ax+ay；
（2）x2+2xy+y2-1＝x（x+2y）+（y +1）（y-1）；
（3）ax2-9a＝a（x+3）（x-3）；
（4）x2+2+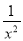
=
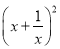
（5）2a3＝2a·a·a.
见解析
【解析】试题分析：根据因式分解的定义判断即可.
试题解析：
因为(1) (2)的右边都不是整式的积的形式.所以它们不是分解因式；(4)中， 都不是整式，(5)中的2a3不是多项式，所以它们也不是分解因式．只有(3)的左边是多项式，右边是整式的积的形式，所以(3)是分解因式.