题目内容
二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是( )
A. k＜－3 B. k＞－3 C. k＜3 D. k＞3
D
【解析】试题分析：∵当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，
∴此时y=|ax2+bx+c|=ax2+bx+c，
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，
∵当ax2+bx+c＜0时，y=ax2+bx+c（a≠0）的图象在x轴下方，
∴此时y=|ax2+bx+c|=﹣（ax2+b...
练习册系列答案
阅读快车系列答案
相关题目
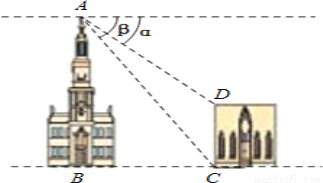
如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为 m（结果不作近似计算）．
【解析】
试题分析：过点D作DE⊥AB于点E，
则四边形BCDE是矩形，
根据题意得：∠ACB=β=60°，∠ADE=α=30°，BC=18m，
∴DE=BC=18m，CD=BE，
在Rt△ABC中，AB=BC•tan∠ACB=18×tan60°=18（m），
在Rt△ADE中，AE=DE•tan∠ADE=18×tan30°=6（m），
∴DC=BE=AB... 已知函数y=kx2-7x-7的图象和x轴有交点，则k的取值范围是__________
【解析】【解析】
分两种情况讨论：①若k=0，则y=-7x-7是一次函数，与x轴有交点；
②若k≠0，则函数y=kx2-7x-7是二次函数．∵二次函数y=kx2﹣7x﹣7的图象和x轴有交点，∴，∴k≥且k≠0．
综上所述：k≥．故答案为：k≥． 二次函数y＝x2＋bx＋c的图象经过点(4，3)，(3，0)．
(1)求b、c的值；
(2)求出该二次函数图象的顶点坐标和对称轴；
(3)画出二次函数y＝x2＋bx＋c的图象．
(1)b＝－4，c＝3；(2) (2，－1)，x＝2；(3)画图见解析.
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；
（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式；
（3）采用列表、描点法画出图象即可．
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴
解得
... 二次函数y＝x2－(m－4)x－m的图象与x轴的两个交点关于y轴对称，则其顶点坐标为___________．
(0，－4)
【解析】根据二次函数y＝x2－(m－4)x－m的图象与x轴的两个交点关于y轴对称，可知抛物线关于y轴对称，所以 =0，解得m=4，则顶点坐标为（0，-4）．
故答案为：（0，-4）. 已知二次函数y＝－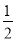
x2－7x＋
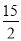，若自变量x分别取x1、x2、x3，且0＜x1＜x2＜x3，则对应的函数值y1、y2、y3的大小关系正确的是( )
A. y1＞y2＞y3 B. y1＜y2＜y3 C. y2＞y3＞y1 D. y2＜y3＜y1
A
【解析】∵二次函数y＝－x2－7x＋，∴此函数的对称轴为：x＝－＝－＝－7.∵0如图所示，一水库迎水坡AB的坡度i=1：2，求坡角α的正弦值sinα
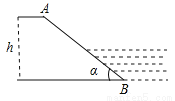
【解析】试题分析：首先过点A作AC⊥BC于点C，设AC=x，根据AC=x，根据坡比可得BC=2x，根据勾股定理求出AB的长度，然后根据正弦的求法得出答案．
试题解析：过A作AC⊥BC于C， ∵AB的坡度i=1：2，
∴tanα=， 设AC=x，BC=2x， 根据勾股定理可得：AB= ，
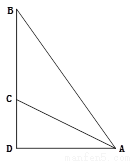
则sinα=． 如图，斜面AC的坡度（CD与AD的比）为1:2，AC=
米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带相连，若AB=10米，则旗杆BC的高度为（ ）
A. 5米 B. 6米 C. 8米 D.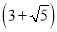 
米
A
【解析】试题分析：根据CD：AD=1:2，AC=3米可得：CD=3米，AD=6米，根据AB=10米，∠D=90°可得：BD==8米，则BC=BD－CD=8－3=5米. 分解因式：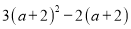 
=______________.
(a+2)(3a+4)
【解析】提取公因式a+2即可，即原式=（a+2）（3a+6-2）=(a+2)(3a+4).