��Ŀ����
ij���̻���Ϊ����4.18�̻����¾�ó�����ر��������һ���������ڣ��������ڵ����ո߶�h(m)�����ʱ��t(s)�Ĺ�ϵʽ��h����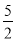 t2��20t��1.���������ڵ�յ���ߵ㴦��������ӵ�����յ�������Ҫ��ʱ��Ϊ( )
t2��20t��1.���������ڵ�յ���ߵ㴦��������ӵ�����յ�������Ҫ��ʱ��Ϊ( )
A. 3s B. 4s C. 5s D. 6s
 B
���������Ѷ��κ�����һ��ʽд�ɶ���ʽh=-t2+20t+1=-��t-4��2+41���ҳ��������꣨4��41������t=4ʱ��������ߵ㣮
��ѡ��B��
B
���������Ѷ��κ�����һ��ʽд�ɶ���ʽh=-t2+20t+1=-��t-4��2+41���ҳ��������꣨4��41������t=4ʱ��������ߵ㣮
��ѡ��B��
 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д���ͼ��ij��¥������һ�źŷ��������ھ��ν�����ABCD��A��C�����ø�������F�����Ƿֱ�Ϊ45���60�㣬���ν��������AD��20 m���߶�DC��30 m�����źŷ��������˵�����ĸ߶�(��FG�ij�)Ϊ( )
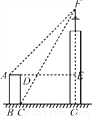
A. (35 ��55)m B. (25
��55)m B. (25 ��45)m C. (25
��45)m C. (25 ��75)m D. (50��20
��75)m D. (50��20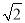 )m
)m
 C
����������CG=xm,��ͼ����֪��:EF=(x+20) ��,FG=x��,
��(x+20) ��+30= x��,
�����x=,
��FG= x��==m,
��ѡC.
C
����������CG=xm,��ͼ����֪��:EF=(x+20) ��,FG=x��,
��(x+20) ��+30= x��,
�����x=,
��FG= x��==m,
��ѡC. ��֪���κ���y=��x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η��̩�x2+2x+m=0�Ľ�Ϊ_____��

 x1=4��x2=��2
������������������ɶ��κ���y=��x2+2x+m�IJ���ͼ����Եõ������ߵĶԳ������������x���һ���������꣬Ȼ����������һ���������꣬��������������x�ύ��ĺ���������Ӧ��һԪ���η��̵ĸ��Ĺ�ϵ���ɵõ�����x��һԪ���η��̩�x2+2x+m=0�Ľ⣮
��������
������ö��κ���y=��x2+2x+m�ĶԳ���Ϊx=1����x���һ������Ϊ��3��0����
��������...
x1=4��x2=��2
������������������ɶ��κ���y=��x2+2x+m�IJ���ͼ����Եõ������ߵĶԳ������������x���һ���������꣬Ȼ����������һ���������꣬��������������x�ύ��ĺ���������Ӧ��һԪ���η��̵ĸ��Ĺ�ϵ���ɵõ�����x��һԪ���η��̩�x2+2x+m=0�Ľ⣮
��������
������ö��κ���y=��x2+2x+m�ĶԳ���Ϊx=1����x���һ������Ϊ��3��0����
��������... ��ѡ��һ����ϲ����a��b��c��ֵ��ʹ���κ���y��ax2��bx��c(a��0)��ͼ��ͬʱ��������������(1)�������£�(2)��x��2ʱ��y��x�����������x��2ʱ��y��x���������С�������Ķ��κ����Ľ���ʽ������____________.
 �𰸲�Ψһ��ֻҪ����b����4a��a��0���ɣ���y����x2��4x��3��y����2x2��8x��3�ȣ�
�������������������ϸ��������Ҫ����ݶ��κ��������ʼ��ɵõ����.
�𰸲�Ψһ����y����(x��1)2��y����(x��1)2��2��
�𰸲�Ψһ��ֻҪ����b����4a��a��0���ɣ���y����x2��4x��3��y����2x2��8x��3�ȣ�
�������������������ϸ��������Ҫ����ݶ��κ��������ʼ��ɵõ����.
�𰸲�Ψһ����y����(x��1)2��y����(x��1)2��2�� ij������һ�·��²�Ʒ���з��ʽ�ΪaԪ���Ժ�ÿ���²�Ʒ���з��ʽ���������������ʶ���x����ó��������·��²�Ʒ���з��ʽ�y(Ԫ)����x�ĺ�����ϵʽΪ____��
 y��a(1��x)2
�������������������һ�·��²�Ʒ���з��ʽ�ΪaԪ��
2�·���ÿ���²�Ʒ���з��ʽ���������������ʶ���x��
��2�·��з��ʽ�Ϊ�������·ݵ��з��ʽ�Ϊ��
�ʴ�Ϊ�� ��
y��a(1��x)2
�������������������һ�·��²�Ʒ���з��ʽ�ΪaԪ��
2�·���ÿ���²�Ʒ���з��ʽ���������������ʶ���x��
��2�·��з��ʽ�Ϊ�������·ݵ��з��ʽ�Ϊ��
�ʴ�Ϊ�� �� ������y��2(x��3)2��1�Ķ���������( )
A. (3��1) B. (3����1) C. (��3��1) D. (��3����1)
 A
�����������������߶���ʽ���ص�ֱ��д�����������ǣ�h��k������֪������y��2(x��3)2��1�Ķ��������ǣ�3��1����
��ѡ��A��
A
�����������������߶���ʽ���ص�ֱ��д�����������ǣ�h��k������֪������y��2(x��3)2��1�Ķ��������ǣ�3��1����
��ѡ��A�� ��ͼ����С�����¶�i=1��5��������B��A������26��ʱ��С��ʵ�������߶�AC=_________�ף��������ø��ű�ʾ��

 ����������������������¶ȵĶ������AC=x��BC=5x���ٸ��ݹ��ɶ��������з������.
��������AC=x��BC=5x����ã�
��С��ʵ�������߶���.
����������������������¶ȵĶ������AC=x��BC=5x���ٸ��ݹ��ɶ��������з������.
��������AC=x��BC=5x����ã�
��С��ʵ�������߶���. ��ͼ��Ϊ��ȫ�����������ӳ����ݣ�������б����45�㽵��30�㣮��֪����AB�ij�Ϊ3m����D��B��C��ͬһˮƽ�����ϣ���ô�ӳ���Ļ���AD�ij��ǣ�������
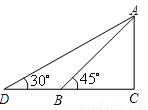
A. 2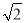 B.
B. 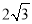 C.
C. 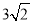 D.
D. 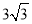
 C
���������������������AB�ij����Լ���ABC�����Ǻ����ɵã�AC=�ף�����Rt��ADC�С�D������ֵ�ɵã�AD=2AC=�ף���ѡC��
C
���������������������AB�ij����Լ���ABC�����Ǻ����ɵã�AC=�ף�����Rt��ADC�С�D������ֵ�ɵã�AD=2AC=�ף���ѡC�� ��֪x2-2x-3=0�������ʽ6-2x2+4x��ֵ�Ƕ��٣�
 0.
�������������������֪x2-2x-3=0���ɵ�x2-2x=3���Ѵ���ʽ6-2x2+4x��Ϊ6-2��x2-2x����������ֵ����.
���������
��x2-2x-3=0��
��x2-2x=3��
��6-2x2+4x=6-2��x2-2x��=6-2��3=0.
0.
�������������������֪x2-2x-3=0���ɵ�x2-2x=3���Ѵ���ʽ6-2x2+4x��Ϊ6-2��x2-2x����������ֵ����.
���������
��x2-2x-3=0��
��x2-2x=3��
��6-2x2+4x=6-2��x2-2x��=6-2��3=0. 
