题目内容
小明乘滑草车沿坡比为1：2.4的斜坡下滑130米，求他下降的高度
50米
【解析】试题分析：根据坡比可设BC=x，AC=2.4x，根据勾股定理得出AB=2.6x，根据AB的长度得出x的值，从而得出BC的值，即下降的高度．
试题解析：∵坡比为1：2.4， ∴BC：AC=1：2.4， 设BC=x，AC=2.4x，
则AB= ∵AB=130米， ∴x=50， 则BC=x=50（米）．
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y（元/千度））与电价x（元/千度）的函数图象如图：
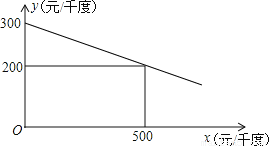
（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？
（2）为了实现节能减排目标，有关部门规定，该厂电价x（元/千度）与每天用电量m（千度）的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
（1）工厂消耗每千度电产生利润是180元（2）当工厂每天消耗50千度电时，工厂每天消耗电产生利润为5000元
【解析】试题分析：（1）设y=kx+b（k≠0），利用待定系数法求一次函数解析式解答即可；
（2）根据利润=每天的用电量×每千度电产生利润y，然后整理得到W与m的关系式，再根据二次函数的最值问题解答．
【解析】
（1）设工厂每千度电产生利润y（元/千度）与电价x（元/千... 在二次函数y＝ax2＋bx＋c中，若a与c异号，则其图象与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
A
【解析】【解析】
∵a与c异号，∴ac＜0，∴△=＞0，∴二次函数图象与x轴的交点个数为2．故选A． 如图，对称轴平行于y轴的抛物线与x轴交于(1，0)、(3，0)两点，则它的对称轴为____________________．
直线x＝2
【解析】试题分析：当两点到对称轴距离相等时，则所对应的函数值相等，则二次函数的对称轴为：x==2. 已知抛物线y＝x2－2x＋m＋1与x轴有两个不同的交点，则函数y＝
的大致图象是( )
A. （A） B. （B） C. （C） D. （D）
A
【解析】抛物线y=x2-2x+m+1与x轴有两个不同的交点，可得△=（-2）2-4（m+1）＞0，解得m＜0，因此可得函数y=的图象位于二、四象限，
故选：A． 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图．其中AB、CD分别表示地下广场、地面广场电梯口处的水平线．已知∠ABC=135°，BC的长约是6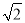
m，则乘电梯从点B到点C上升的高度h是_________．
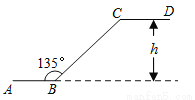
6m
【解析】试题分析：
过点C作CM⊥AB交AB的延长线于点M, 由∠ABC=135°可得∠CBM=45°，在Rt△BMC中，由锐角三角函数即可求得CM=6． 拦水坝横断面如图所示,迎水坡AB的坡比是1∶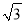
,坝高BC=10 m,则坡面AB的长度是( )
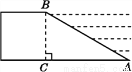
A. 15 m B. 20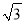
m C. 10
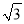m D. 20 m
D
【解析】在Rt△ABC中，BC＝10m， ，∴ (m)，
∴．故选D． 如果水流的速度为a m/min(定量)，那么每分钟的进水量Q(m3)与所选择的水管直径D(m)之间的函数关系式是什么?
Q＝.
【解析】试题分析：根据圆柱体的体积公式V=πr2h，直接代入求解即可.
试题解析：函数关系式为Q＝a·π·()2＝ . 把一个多项式化成几个________的_______的形式，叫做把这个多项式分解因式.
整式 积
【解析】根据因式分解的定义可得：把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.