题目内容
抛物线y＝2(x－3)2＋1的顶点坐标是( )
A. (3，1) B. (3，－1) C. (－3，1) D. (－3，－1)
A
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y＝2(x－3)2＋1的顶点坐标是（3，1）．
故选：A．
已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．
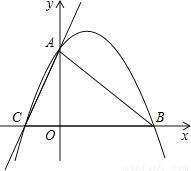
（1）求过A、B、C三点的抛物线的解析式；
（2）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．
（1）y= -x2+2x+3（2）存在,（）
【解析】试题分析：（1）求得直线y=3x+3与坐标轴的两交点坐标，然后根据OB=OA即可求得点B的坐标，然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可；
（2）首先利用待定系数法求得直线AB的解析式，然后根据CD∥AB得到两直线的k值相等，根据直线CD经过点C求得直线CD的解析式，然后求得直线CD和抛物线的交点坐标即可；
... 根据下列表格的对应值：
判断方程 ax2＋bx＋c=0(a≠0，a，b，c为常数)的一个解x的取值范围是( )
A. 3＜x＜3.23 B. 3．23＜x＜3.24 C. 3.24＜x＜3.25 D. 3.25＜x＜3.26
C
【解析】【解析】
函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根，函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0；
由表中数据可知：y=0在y=﹣0.02与y=0.03之间，∴对应的x的值在3.24与3.25之间，即3.24＜x＜3.25．故选C． 已知下列函数：①y＝x2；②y＝－x2；③y＝(x－1)2＋2.其中图象通过平移可以得到函数y＝x2＋2x－3的图象的有_____________(填写所有正确选项的序号)．
①③
【解析】把函数y=x2+2x-3整理成顶点式解析式y=（x+1）2-4，得到y=x2+2x-3的顶点坐标为（-1，-4），然后根据顶点的变化确定出：
①y=x2向左平移1个单位，向下4个单位，得到y=x2+2x-3；
②y=x2不能平移得到y=x2+2x-3；
③y=（x-1）2+2向左平移2个单位，向下平移6个单位得到y=x2+2x-3，
所以，①③图象通过平移可以得到函... 某市烟花厂为该市4.18烟花三月经贸旅游特别设计制作一种新型礼炮，这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h＝－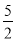
t2＋20t＋1.若这种礼炮点火开空到最高点处引爆，则从点火升空到引爆需要的时间为( )
A. 3s B. 4s C. 5s D. 6s
B
【解析】把二次函数的一般式写成顶点式h=-t2+20t+1=-（t-4）2+41，找出顶点坐标（4，41），当t=4时，升到最高点．
故选：B． 两棵树种在倾角为24°36′的斜坡上，它们的坡面距离是4米，求它们之间的水平距离（可用计算器计算，精确到0.1米）
3.6米
【解析】试题分析：根据题意可知倾角为24°36′，即坡角为24°36′，
利用余弦关系cos24°36′==0.909，
可求出它们之间的水平距离为：水平距离≈3.6米． 如图，一河坝的横断面为等腰梯形ABCD，坝顶宽10米，坝高12米，斜坡AB的坡度i＝1∶1.5，则坝底AD的长度为( )
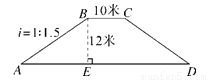
A. 26米 B. 28米 C. 30米 D. 46米
D
【解析】∵坝高12米，斜坡AB的坡度i=1：1.5，
∴AE=1.5BE=18米，
∵BC=10米，
∴AD=2AE+BC=2×18+10=46米，
故选D． 一台机器原价60万元，如果每年的折旧率是x，两年后这台机器的价位约为y万元，求y与x的函数关系式.
【解析】
试题分析：根据每年的折旧率是x可得一年后的价位为，两年后的价位为.
由题意得y与x的函数关系式为 (x+3)2=x2+6x+9从左到右的变形是_________________.
整式乘法
【解析】根据完全平方公式计算出(x+3)2的结果，属于整式的乘法.