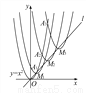
如图，抛物线y＝x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1、A2、A3…An，….将抛物线y＝x2沿直线L：y＝x向上平移，得一系列抛物线，且满足下列条件：①抛物线的顶点M1、M2、M3、…Mn，…都在直线L：y＝x上；②抛物线依次经过点A1、A2、A3…An、….则顶点M2014的坐标为______________．
(4027，4027)
【解析】试题解析：M1（a1，a 1）是抛物线y1=（x- a 1）2+a1的顶点，
抛物线y=x2与抛物线y1=（x- a 1）2+ a 1相交于A1，
得x2=（x- a 1）2+ a 1，
即2a1x= a 12+ a 1，
x=（a1+1）．
∵x为整数点
∴a1=1，
M1（1，1）；
M2（a2，a 2）是抛... 二次函数y＝x2＋bx＋c的图象经过点(4，3)，(3，0)．
(1)求b、c的值；
(2)求出该二次函数图象的顶点坐标和对称轴；
(3)画出二次函数y＝x2＋bx＋c的图象．
(1)b＝－4，c＝3；(2) (2，－1)，x＝2；(3)画图见解析.
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；
（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式；
（3）采用列表、描点法画出图象即可．
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴
解得
... 已知函数y＝mx2－6x＋1(m是常数)．
(1)求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
(2)若该函数的图象与x轴只有一个交点，求m的值．
（1）证明见解析；（2）m的值为0或9.
【解析】试题分析：（1）根据解析式可知，当x=0时，与m值无关，故可知不论m为何值，函数y= ﹣6x+1的图象都经过y轴上一个定点（0，1）．
（2）应分两种情况讨论：①当函数为一次函数时，与x轴有一个交点；
②当函数为二次函数时，利用根与系数的关系解答．
试题解析：（1）当x=0时，y=1．
所以不论m为何值，函数y= ﹣6... 如图，在平面直角坐标系中，O是坐标原点，点A的坐标是(－2，4)，过点A作AB⊥y轴，垂足为B，连接OA.
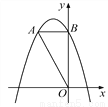
(1)求△OAB的面积；
(2)若抛物线y＝－x2－2x＋c经过点A.
①求c的值；
②将抛物线向下平移m个单位长度，使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界)，求m的取值范围(直接写出答案即可)．
（1）4；（2）①c＝4；②m的取值范围为1＜m＜3.
【解析】（1）根据点A的坐标是（-2，4），得出AB，BO的长度，即可得出△OAB的面积；
（2）①把点A的坐标（-2，4）代入y=-x2-2x+c中，直接得出即可；
②利用配方法求出二次函数解析式即可得出顶点坐标，根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围．
【解析】
（1）∵点A的坐标是（-2，4）... 某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系：
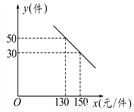
(1)求出y与x之间的函数关系式；
(2)写出每天的利润W与销售单价x之间的函数关系式；若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？
（1）y＝－x＋180；（2）售价定为140元/件时，每天最大利润W＝1600元．
【解析】（1）设y与x之间的函数关系式为y=kx+b（k≠0），根据所给函数图象列出关于kb的关系式，求出k、b的值即可；
（2）把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式，由此关系式即可得出结论．
【解析】
（1）设y与x之间的函数关系式为y=kx+b（k≠0），由所给... 如图，矩形ABCD的两边长AB＝18cm，AD＝4cm.点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动，设运动时间为x秒，△PBQ的面积为y(cm2)．
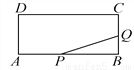
(1)求y关于x的函数关系式，并写出x的取值范围；
(2)求△PBQ的面积的最大值．
（1）y＝－x2＋9x(0＜x≤4)；（2）△PBQ的面积的最大值是20cm2.
【解析】试题分析：（1）分别表示出PB、BQ的长，然后根据三角形的面积公式列式整理即可得解；
（2）把函数关系式整理成顶点式解析式，然后根据二次函数的最值问题解答．
试题解析：（1）∵S△PBQ＝PB·BQ，
PB＝AB－AP＝18－2x，
BQ＝x，
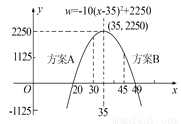
∴y＝ (18－2x)x，... 某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
(1)写出商场销售这种工具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；
(2)求销售单价为多少元时，该文具每天的销售利润最大；
(3)商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元．
请比较哪种方案的最大利润更高，并说明理由．
（1）w＝－10x2＋700x－10000；
（2）销售单价为35元时，每天销售利润最大，最大利润为2250元；
（3）方案A的最大利润更高，理由见解析.
【解析】试题分析：（1）根据利润=（销售单价-进价）×销售量，列出函数关系式即可；
（2）根据（1）式列出的函数关系式，运用配方法求最大值；
（3）分别求出方案A、B中x的取值范围，然后分别求出A、B方案的最大利润... 如图，已知抛物线y＝
x2－
x－3与x轴的交点为A、D(A在D的右侧)，与y轴的交点为C.
(1)直接写出A、D、C三点的坐标；
(2)若点M在抛物线上，使得△MAD的面积与△CAD的面积相等，求点M的坐标；
(3)设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．
（1）A点坐标为(4，0)，D点坐标为(－2，0)，C点坐标为(0，－3)；
（2）M点坐标为(2，－3)或(1＋，3)或(1－，3)；
（3）在抛物线上存在一点P，使得以点A、B、C、P四点为顶点所构成的四边形为梯形；点P的坐标为(－2，0)或(6，6)．
【解析】试题分析：（1）在中令，解得，
∴A(4，0) 、D(－2，0).
在中令，得，∴C(0，－3).
... 如图所示的是二次函数y＝ax2＋bx＋c的图象，则一次函数y=ax－b的图象不经过( )
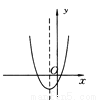
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
B
【解析】【解析】
由图象开口向上可知a＞0，对称轴x=＜0，得b＞0．所以一次函数y=y=ax﹣b的图象经过第一、三、四象限，不经过第二象限．故选B． 在二次函数y＝ax2＋bx＋c中，若a与c异号，则其图象与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
A
【解析】【解析】
∵a与c异号，∴ac＜0，∴△=＞0，∴二次函数图象与x轴的交点个数为2．故选A．