题目内容
某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
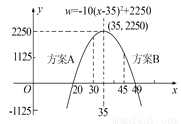
(1)写出商场销售这种工具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；
(2)求销售单价为多少元时，该文具每天的销售利润最大；
(3)商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元．
请比较哪种方案的最大利润更高，并说明理由．
（1）w＝－10x2＋700x－10000；
（2）销售单价为35元时，每天销售利润最大，最大利润为2250元；
（3）方案A的最大利润更高，理由见解析.
【解析】试题分析：（1）根据利润=（销售单价-进价）×销售量，列出函数关系式即可；
（2）根据（1）式列出的函数关系式，运用配方法求最大值；
（3）分别求出方案A、B中x的取值范围，然后分别求出A、B方案的最大利润...
用反证法证明命题“对顶角相等”第一步假设__________________.
对顶角不相等
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，即先假设“对顶角不相等”． 将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品的零售价每降价1元，其日销量就增加1个，为了获取每日最大利润，则应降价（ ）
A. 5元 B. 10元 C. 15元 D. 20元
A
【解析】设应降价x元，总利润为y元，根据题意可得：
，
化简、配方得：
，
∴当时，y最大=625，
∴ B、C、D错误，选A. 已知函数y=kx2-7x-7的图象和x轴有交点，则k的取值范围是__________
【解析】【解析】
分两种情况讨论：①若k=0，则y=-7x-7是一次函数，与x轴有交点；
②若k≠0，则函数y=kx2-7x-7是二次函数．∵二次函数y=kx2﹣7x﹣7的图象和x轴有交点，∴，∴k≥且k≠0．
综上所述：k≥．故答案为：k≥． 函数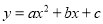
的图象如图，那么关于x的方程
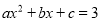的根的情况是（ ）
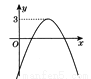
A. 有两个不相等的实数根 B. 有两个异号实数根
C. 有两个相等实数根 D. 无实数根
C
【解析】【解析】
将函数y=ax2+bx+c的图象往下平移3个单位即可得出函数y=ax2+bx+c﹣3的图象．∵函数y=ax2+bx+c的图象开口向下，顶点纵坐标为3，∴函数y=ax2+bx+c﹣3的图象与x轴只有一个交点，∴方程ax2+bx+c﹣3=0有两个相等的实数根．
故答案为：方程ax2+bx+c﹣3=0有两个相等的实数根． 二次函数y＝x2＋bx＋c的图象经过点(4，3)，(3，0)．
(1)求b、c的值；
(2)求出该二次函数图象的顶点坐标和对称轴；
(3)画出二次函数y＝x2＋bx＋c的图象．
(1)b＝－4，c＝3；(2) (2，－1)，x＝2；(3)画图见解析.
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；
（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式；
（3）采用列表、描点法画出图象即可．
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴
解得
... 二次函数y＝x2－(m－4)x－m的图象与x轴的两个交点关于y轴对称，则其顶点坐标为___________．
(0，－4)
【解析】根据二次函数y＝x2－(m－4)x－m的图象与x轴的两个交点关于y轴对称，可知抛物线关于y轴对称，所以 =0，解得m=4，则顶点坐标为（0，-4）．
故答案为：（0，-4）. 如图所示，一水库迎水坡AB的坡度i=1：2，求坡角α的正弦值sinα
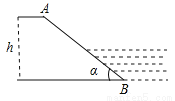
【解析】试题分析：首先过点A作AC⊥BC于点C，设AC=x，根据AC=x，根据坡比可得BC=2x，根据勾股定理求出AB的长度，然后根据正弦的求法得出答案．
试题解析：过A作AC⊥BC于C， ∵AB的坡度i=1：2，
∴tanα=， 设AC=x，BC=2x， 根据勾股定理可得：AB= ，
则sinα=． 先化简，再求值：
已知串联电路的电压U＝IR1+IR2+IR3，当R1＝12.9，R2=18.5，R3=18.6，I=2.3时，求U的值。
115
【解析】试题分析：先根据提取公因式分解U＝IR1+IR2+IR3，再代入求值即可得到结果.
U=I(R1+R2+R3)=2.3×(12.9+18.5+18.6)=2.3×50=115.