题目内容
如图所示的是二次函数y＝ax2＋bx＋c的图象，则一次函数y=ax－b的图象不经过( )
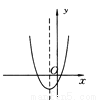
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
B
【解析】【解析】
由图象开口向上可知a＞0，对称轴x=＜0，得b＞0．所以一次函数y=y=ax﹣b的图象经过第一、三、四象限，不经过第二象限．故选B．
练习册系列答案
相关题目
已知△ABC中，AB＝AC，求证∠B＜90°，下面写出了用反证法证明过程中的四个步骤：①所以∠B＋∠C＋∠A＞180°，这与三角形内角和定理相矛盾；②所以∠B＜90°；③假设∠B≥90°；④那么由AB＝AC，得∠B＝∠C≥90°，即∠B＋∠C≥180°.这四个步骤正确的顺序应是_________(填序号)．
③④①②
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，然后根据已知条件得出与定理相矛盾，最后得出假设不成立，得出答案，故正确的序号是：③④①②． 如图所示，桥拱是抛物线形，其函数的表达式为y= -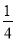
x2，当水位线在AB位置时，水面宽12m，这时水面离桥顶的高度为（ ）
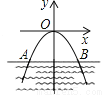
A. 3m B.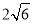 
m C.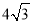 
m D. 9 m
D
【解析】试题解析：由已知知：
点的横坐标为.
把代入
得
即水面离桥顶的高度为
故选D. 已知二次函数y=-x2+4x-3，其图象与y轴交于点B，与x轴交于A，C 两点.求△ABC的周长和面积.
C△ABC=，S△ABC=3.
【解析】试题分析：先分别求得二次函数的图象与坐标轴的交点坐标，再根据勾股定理求得△ABC的三边长，即可得到△ABC的周长，再根据三角形的面积公式即可求得结果.
令x=0,得y=-3,故B点坐标为(0,-3).
解方程-x2+4x-3=0,得x1=1,x2=3.
故A、C两点的坐标为(1,0),(3,0).
所以AC=3-1=2,AB=,... 函数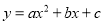
的图象如图所示，则下列结论错误的是（ ）
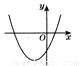
A. a＞0 B. b2－4ac＞0
C.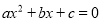 
的两根之和为负 D. 
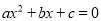的两根之积为正
D
【解析】【解析】
∵抛物线开口向上，∴a＞0，故A正确．
∵抛物线与x轴有两个交点，∴b2－4ac＞0，故B正确．
由图象可知， 一根为正，一根为负，且负根的绝对值大于正根的绝对值，∴两根之和为负，两根之积为负，故C正确，D错误．
故选D． 如图，在平面直角坐标系中，O是坐标原点，点A的坐标是(－2，4)，过点A作AB⊥y轴，垂足为B，连接OA.
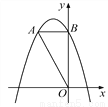
(1)求△OAB的面积；
(2)若抛物线y＝－x2－2x＋c经过点A.
①求c的值；
②将抛物线向下平移m个单位长度，使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界)，求m的取值范围(直接写出答案即可)．
（1）4；（2）①c＝4；②m的取值范围为1＜m＜3.
【解析】（1）根据点A的坐标是（-2，4），得出AB，BO的长度，即可得出△OAB的面积；
（2）①把点A的坐标（-2，4）代入y=-x2-2x+c中，直接得出即可；
②利用配方法求出二次函数解析式即可得出顶点坐标，根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围．
【解析】
（1）∵点A的坐标是（-2，4）... 已知二次函数y＝－x2＋4，当－2≤x≤3时，函数的最小值是_____，最大值是____．
－5 4
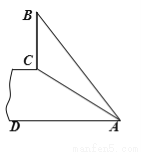
【解析】试题解析：抛物线y＝－x2＋4，开口向下，有最大值为4，当x=3时有最小值为-5. 如图，斜坡AC的坡度（坡比）为1: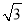 
，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．
6米.
【解析】
试题分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．
试题解析：延长BC交AD于E点，则CE⊥AD．
在Rt△AEC中，AC=10，由坡比为1：可知：∠CAE=30°，
∴... 课外拓展：不解方程组
，求
的值.
6
【解析】试题分析：把因式分解后整体代入求值即可.
试题解析：
∵x-3y=1，2x+y=6，
∴
=
=（x-3y）2（7y+2x-6y）
=（x-3y）2（y+2x），
=1×6=6.