题目内容
已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
 (1)证明见解析;(2)m的值为0或9.
【解析】试题分析:(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y= ﹣6x+1的图象都经过y轴上一个定点(0,1).
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
试题解析:(1)当x=0时,y=1.
所以不论m为何值,函数y= ﹣6...
(1)证明见解析;(2)m的值为0或9.
【解析】试题分析:(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y= ﹣6x+1的图象都经过y轴上一个定点(0,1).
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
试题解析:(1)当x=0时,y=1.
所以不论m为何值,函数y= ﹣6...
练习册系列答案
相关题目
周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是()m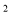

A. 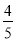 B.
B. 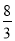 C. 4 D.
C. 4 D. 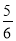
 B
【解析】设窗户的宽是x,根据题意得
S=
=
∴当窗户宽是m时,面积最大是m²,故选B.
B
【解析】设窗户的宽是x,根据题意得
S=
=
∴当窗户宽是m时,面积最大是m²,故选B. 不论m为何实数,抛物线y=x2-mx+m-2( )
A.在x轴上方 B.与x轴只有一个交点
C.与x轴有两个交点 D.在x轴下方
 C
【解析】
试题分析:,当△=-4ac>0时,函数与x轴有两个交点;当△=-4ac=0时,函数与x轴有一个交点;当△=-4ac<0时,函数与x轴没有交点.根据题意可得:△=-4(m-2)=+4>0,则函数与x轴有两个交点.
C
【解析】
试题分析:,当△=-4ac>0时,函数与x轴有两个交点;当△=-4ac=0时,函数与x轴有一个交点;当△=-4ac<0时,函数与x轴没有交点.根据题意可得:△=-4(m-2)=+4>0,则函数与x轴有两个交点. 如图,已知抛物线y= x2-
x2- x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.

(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
 (1)A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
(2)M点坐标为(2,-3)或(1+,3)或(1-,3);
(3)在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(-2,0)或(6,6).
【解析】试题分析:(1)在中令,解得,
∴A(4,0) 、D(-2,0).
在中令,得,∴C(0,-3).
...
(1)A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
(2)M点坐标为(2,-3)或(1+,3)或(1-,3);
(3)在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(-2,0)或(6,6).
【解析】试题分析:(1)在中令,解得,
∴A(4,0) 、D(-2,0).
在中令,得,∴C(0,-3).
... 开口向下的抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),则m=_____.
 -1
【解析】由于抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),
∴对称轴为直线x=-1,x==-1,
解得m1=-1,m2=2.
由于抛物线的开口向下,所以当m=2时,m2-2=2>0,不合题意,应舍去,
∴m=-1.
故答案为:-1.
-1
【解析】由于抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),
∴对称轴为直线x=-1,x==-1,
解得m1=-1,m2=2.
由于抛物线的开口向下,所以当m=2时,m2-2=2>0,不合题意,应舍去,
∴m=-1.
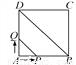
故答案为:-1. 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可以用图象表示为( )
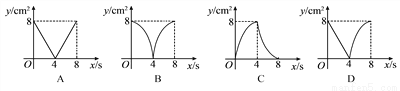
A. (A) B. (B) C. (C) D. (D)
 B
【解析】试题分析:根据题意结合图形,分情况讨论:
①0≤x≤4时,根据四边形PBDQ的面积=△ABD的面积﹣△APQ的面积,列出函数关系式,从而得到函数图象;
②4≤x≤8时,根据四边形PBDQ的面积=△BCD的面积﹣△CPQ的面积,列出函数关系式,从而得到函数图象,再结合四个选项即可得解.
【解析】
①0≤x≤4时,
∵正方形的边长为4cm,
∴y=S△...
B
【解析】试题分析:根据题意结合图形,分情况讨论:
①0≤x≤4时,根据四边形PBDQ的面积=△ABD的面积﹣△APQ的面积,列出函数关系式,从而得到函数图象;
②4≤x≤8时,根据四边形PBDQ的面积=△BCD的面积﹣△CPQ的面积,列出函数关系式,从而得到函数图象,再结合四个选项即可得解.
【解析】
①0≤x≤4时,
∵正方形的边长为4cm,
∴y=S△... 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1: 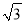 则AB的长为_______
则AB的长为_______

 12米
【解析】试题分析:根据BC=6m,坡比为1: 可得:AC=6m,最后根据Rt△ABC的勾股定理可得:AB=12米.
12米
【解析】试题分析:根据BC=6m,坡比为1: 可得:AC=6m,最后根据Rt△ABC的勾股定理可得:AB=12米. 如果x+y=5,xy=2,求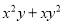 和
和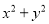 的值
的值
 10;21.
【解析】试题分析:(1)因式分解后直接代入求值即可;(2)化为(x+y)2-2xy后代入求值即可.
试题解析:
∵x+y=5,xy=2,
∴=xy(x+y)=2×5=10;
=(x+y)2-2xy=52-2×2=25-4=21.
10;21.
【解析】试题分析:(1)因式分解后直接代入求值即可;(2)化为(x+y)2-2xy后代入求值即可.
试题解析:
∵x+y=5,xy=2,
∴=xy(x+y)=2×5=10;
=(x+y)2-2xy=52-2×2=25-4=21. 
