题目内容
如图,矩形ABCD的两边长AB=18cm,AD=4cm.点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x秒,△PBQ的面积为y(cm2).
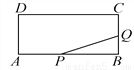
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
 (1)y=-x2+9x(0<x≤4);(2)△PBQ的面积的最大值是20cm2.
【解析】试题分析:(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.
试题解析:(1)∵S△PBQ=PB·BQ,
PB=AB-AP=18-2x,
BQ=x,
∴y= (18-2x)x,...
(1)y=-x2+9x(0<x≤4);(2)△PBQ的面积的最大值是20cm2.
【解析】试题分析:(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.
试题解析:(1)∵S△PBQ=PB·BQ,
PB=AB-AP=18-2x,
BQ=x,
∴y= (18-2x)x,...
如图,四边形ABCD沿直线l对折后互相重合,如果AD∥BC,那么△ABC___(填“是”或“不是”)等腰三角形.
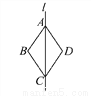
 是
【解析】试题分析:根据折叠图形的性质可知:∠BAC=∠DAC,根据平行线的性质可知:∠DAC=∠ACB,则∠BAC=∠ACB,即△ABC为等腰三角形.
是
【解析】试题分析:根据折叠图形的性质可知:∠BAC=∠DAC,根据平行线的性质可知:∠DAC=∠ACB,则∠BAC=∠ACB,即△ABC为等腰三角形. 向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A. 第8秒 B. 第10秒 C. 第12秒 D. 第15秒
 B
【解析】试题分析:炮弹在第7秒与第14秒时的高度相等所以抛物线的对称轴是在第10秒处,所以在第10秒处高度是最高的.
故选B.
B
【解析】试题分析:炮弹在第7秒与第14秒时的高度相等所以抛物线的对称轴是在第10秒处,所以在第10秒处高度是最高的.
故选B. 若二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点,则这个交点的坐标是_____.
 (-,0)
【解析】【解析】
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点,∴△=b2-4ac=0,∴,令y=0,解得: .故答案为:(,0).
(-,0)
【解析】【解析】
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点,∴△=b2-4ac=0,∴,令y=0,解得: .故答案为:(,0). 根据下列表格的对应值:

判断方程 ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的取值范围是( )
A. 3<x<3.23 B. 3.23<x<3.24 C. 3.24<x<3.25 D. 3.25<x<3.26
 C
【解析】【解析】
函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0;
由表中数据可知:y=0在y=﹣0.02与y=0.03之间,∴对应的x的值在3.24与3.25之间,即3.24<x<3.25.故选C.
C
【解析】【解析】
函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0;
由表中数据可知:y=0在y=﹣0.02与y=0.03之间,∴对应的x的值在3.24与3.25之间,即3.24<x<3.25.故选C. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1、A2、A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1、M2、M3、…Mn,…都在直线L:y=x上;②抛物线依次经过点A1、A2、A3…An、….则顶点M2014的坐标为______________.
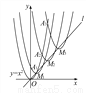
 (4027,4027)
【解析】试题解析:M1(a1,a 1)是抛物线y1=(x- a 1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x- a 1)2+ a 1相交于A1,
得x2=(x- a 1)2+ a 1,
即2a1x= a 12+ a 1,
x=(a1+1).
∵x为整数点
∴a1=1,
M1(1,1);
M2(a2,a 2)是抛...
(4027,4027)
【解析】试题解析:M1(a1,a 1)是抛物线y1=(x- a 1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x- a 1)2+ a 1相交于A1,
得x2=(x- a 1)2+ a 1,
即2a1x= a 12+ a 1,
x=(a1+1).
∵x为整数点
∴a1=1,
M1(1,1);
M2(a2,a 2)是抛... 已知下列函数:①y=x2;②y=-x2;③y=(x-1)2+2.其中图象通过平移可以得到函数y=x2+2x-3的图象的有_____________(填写所有正确选项的序号).
 ①③
【解析】把函数y=x2+2x-3整理成顶点式解析式y=(x+1)2-4,得到y=x2+2x-3的顶点坐标为(-1,-4),然后根据顶点的变化确定出:
①y=x2向左平移1个单位,向下4个单位,得到y=x2+2x-3;
②y=x2不能平移得到y=x2+2x-3;
③y=(x-1)2+2向左平移2个单位,向下平移6个单位得到y=x2+2x-3,
所以,①③图象通过平移可以得到函...
①③
【解析】把函数y=x2+2x-3整理成顶点式解析式y=(x+1)2-4,得到y=x2+2x-3的顶点坐标为(-1,-4),然后根据顶点的变化确定出:
①y=x2向左平移1个单位,向下4个单位,得到y=x2+2x-3;
②y=x2不能平移得到y=x2+2x-3;
③y=(x-1)2+2向左平移2个单位,向下平移6个单位得到y=x2+2x-3,
所以,①③图象通过平移可以得到函... 两棵树种在倾角为24°36′的斜坡上,它们的坡面距离是4米,求它们之间的水平距离(可用计算器计算,精确到0.1米)
 3.6米
【解析】试题分析:根据题意可知倾角为24°36′,即坡角为24°36′,
利用余弦关系cos24°36′==0.909,
可求出它们之间的水平距离为:水平距离≈3.6米.
3.6米
【解析】试题分析:根据题意可知倾角为24°36′,即坡角为24°36′,
利用余弦关系cos24°36′==0.909,
可求出它们之间的水平距离为:水平距离≈3.6米. 已知 ,求
,求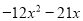 的值.
的值.
 -6
【解析】试题分析:
试题解析:
∵
∴
∴=-3×4x2-21x=-3(2-7x)-21x=-6+21x-21x=-6.
-6
【解析】试题分析:
试题解析:
∵
∴
∴=-3×4x2-21x=-3(2-7x)-21x=-6+21x-21x=-6. 
