��Ŀ����
ij�̳�����һ��ÿ���۸�Ϊ100Ԫ������Ʒ�����̳��������֣����۵���x(Ԫ/��)��ÿ��������y(��)֮��������ͼ��ʾ�Ĺ�ϵ��
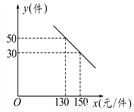
(1)���y��x֮��ĺ�����ϵʽ��
(2)д��ÿ�������W�����۵���x֮��ĺ�����ϵʽ���������̳������ˣ��Ὣ�ۼ۶�Ϊ���٣�����֤ÿ���õ����������������Ƕ��٣�
 ��1��y����x��180����2���ۼ۶�Ϊ140Ԫ/��ʱ��ÿ���������W��1600Ԫ��
����������1����y��x֮��ĺ�����ϵʽΪy=kx+b��k��0����������������ͼ���г�����kb�Ĺ�ϵʽ�����k��b��ֵ���ɣ�
��2����ÿ�������W�����۵���x֮��ĺ�����ϵʽ��Ϊ���κ�������ʽ����ʽ���ɴ˹�ϵʽ���ɵó����ۣ�
��������
��1����y��x֮��ĺ�����ϵʽΪy=kx+b��k��0����������...
��1��y����x��180����2���ۼ۶�Ϊ140Ԫ/��ʱ��ÿ���������W��1600Ԫ��
����������1����y��x֮��ĺ�����ϵʽΪy=kx+b��k��0����������������ͼ���г�����kb�Ĺ�ϵʽ�����k��b��ֵ���ɣ�
��2����ÿ�������W�����۵���x֮��ĺ�����ϵʽ��Ϊ���κ�������ʽ����ʽ���ɴ˹�ϵʽ���ɵó����ۣ�
��������
��1����y��x֮��ĺ�����ϵʽΪy=kx+b��k��0����������...
 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д��ڡ�ABC�У���B��40�㣬��C��70�㣬���ABC���� ������
 ����
�����������⿼����������εķ��ࡣ��C=180��-40��-70�㣽70�㣬���ԡ�A����C=70���Ϊ���������Ρ�
����
�����������⿼����������εķ��ࡣ��C=180��-40��-70�㣽70�㣬���ԡ�A����C=70���Ϊ���������Ρ� ��ͼ�����κ���y= -x2-2x��ͼ����x�ύ�ڵ�A��O��������������һ��P������
S��AOP=3�����P�������ǣ�������
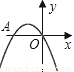
A. ��-3��-3�� B. ��1��-3�� C. ��-3��-3����-3��1�� D. ��-3��-3����1��-3��
 D
�����������������������ߵĽ���ʽ������ȷ����A�����꣬����OA�Ƕ��������ݡ�AOP���������ȷ��P��������ľ���ֵ��������������ߵĽ���ʽ�У��������P������꣮
��𣺡�������
�����ߵĽ���ʽ�У���y=0���ã�-x2-2x=0�����x=0��x=-2��
��A��-2��0����OA=2��
��S��AOP=OA?|yP|=3����|yP|=3��
��P��������Ϊ3ʱ��-x2-...
D
�����������������������ߵĽ���ʽ������ȷ����A�����꣬����OA�Ƕ��������ݡ�AOP���������ȷ��P��������ľ���ֵ��������������ߵĽ���ʽ�У��������P������꣮
��𣺡�������
�����ߵĽ���ʽ�У���y=0���ã�-x2-2x=0�����x=0��x=-2��
��A��-2��0����OA=2��
��S��AOP=OA?|yP|=3����|yP|=3��
��P��������Ϊ3ʱ��-x2-... ��������y=kx2��2x��l��x�����������㣬��k��ȡֵ��Χ��____��
 k��1����k��0
����������������
��y=kx2��2x+1���������k��0��
��������y=kx2��2x+1��ͼ����x�����������㣬�����0��������2��2��4k��0��
��ã�k��1����k��ȡֵ��Χ��k��1��k��0��
�ʴ�Ϊ��k��1��k��0��
k��1����k��0
����������������
��y=kx2��2x+1���������k��0��
��������y=kx2��2x+1��ͼ����x�����������㣬�����0��������2��2��4k��0��
��ã�k��1����k��ȡֵ��Χ��k��1��k��0��
�ʴ�Ϊ��k��1��k��0�� �ڶ��κ���y��ax2��bx��c�У���a��c��ţ�����ͼ����x��Ľ������Ϊ( )
A. 2�� B. 1�� C. 0�� D. ����ȷ��
 A
����������������
��a��c��ţ���ac��0�����=��0������κ���ͼ����x��Ľ������Ϊ2����ѡA��
A
����������������
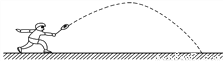
��a��c��ţ���ac��0�����=��0������κ���ͼ����x��Ľ������Ϊ2����ѡA�� 2013��5��26�գ��й���ë��Ӳ����յ������������ھ����ɾ����������ڰ�ҵ����������ë���ij���˶�·�߿��Կ�����һ��������(��ͼ)�����������������أ���ë���н��߶�y(��)��ˮƽ����x(��)֮�������ϵy���� x2��
x2��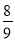 x��
x��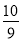 ������ë��ɳ���ˮƽ����Ϊ__________�ף�
������ë��ɳ���ˮƽ����Ϊ__________�ף�
 5
�������������������y=0ʱ��0����
��ã�x1=-1����ȥ����x2=5��
����ë��ɳ���ˮƽ����Ϊ5m��
5
�������������������y=0ʱ��0����
��ã�x1=-1����ȥ����x2=5��
����ë��ɳ���ˮƽ����Ϊ5m�� ��ͼ���Գ���ƽ����y�����������x�ύ��(1��0)��(3��0)���㣬�����ĶԳ���Ϊ____________________��

 ֱ��x��2
����������������������㵽�Գ���������ʱ��������Ӧ�ĺ���ֵ��ȣ�����κ����ĶԳ���Ϊ��x==2.
ֱ��x��2
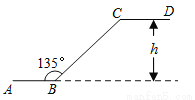
����������������������㵽�Գ���������ʱ��������Ӧ�ĺ���ֵ��ȣ�����κ����ĶԳ���Ϊ��x==2. ��ͼ��ʯ��ɽ�����̳����¹㳡������㳡���ַ�����ʾ��ͼ������AB��CD�ֱ��ʾ���¹㳡������㳡���ݿڴ���ˮƽ�ߣ���֪��ABC=135�㣬BC�ij�Լ��6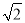 m����˵��ݴӵ�B����C�����ĸ߶�h��_________��
m����˵��ݴӵ�B����C�����ĸ߶�h��_________��
 6m
�����������������
����C��CM��AB��AB���ӳ����ڵ�M, �ɡ�ABC=135��ɵá�CBM=45�㣬��Rt��BMC�У���������Ǻ����������CM=6��
6m
�����������������
����C��CM��AB��AB���ӳ����ڵ�M, �ɡ�ABC=135��ɵá�CBM=45�㣬��Rt��BMC�У���������Ǻ����������CM=6�� �۲����и�ʽ�� 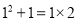 ��
�� 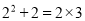 ��
�� 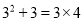 �����������㽫���뵽�Ĺ�������Ȼ��
�����������㽫���뵽�Ĺ�������Ȼ��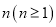 ��ʽ�ӱ�ʾ����_________.
��ʽ�ӱ�ʾ����_________.
 ���������۲�������ʽ�ӣ���������ʽ�ӽ�ʾ�Ĺ��ɣ����ɵ�һ��Ĺ��ɣ� .
���������۲�������ʽ�ӣ���������ʽ�ӽ�ʾ�Ĺ��ɣ����ɵ�һ��Ĺ��ɣ� . 
