��Ŀ����
��ͼ��������y��x2�ڵ�һ�����ھ�����������(�����ꡢ�����궼Ϊ�����ĵ�)����ΪA1��A2��A3��An����.��������y��x2��ֱ��L��y��x����ƽ�ƣ���һϵ�������ߣ������������������������ߵĶ���M1��M2��M3����Mn��������ֱ��L��y��x�ϣ������������ξ�����A1��A2��A3��An����.��M2014������Ϊ______________��
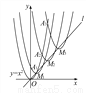
 (4027��4027)
�����������������M1��a1��a 1����������y1=��x- a 1��2+a1�Ķ��㣬
������y=x2��������y1=��x- a 1��2+ a 1�ཻ��A1��
��x2=��x- a 1��2+ a 1��
��2a1x= a 12+ a 1��
x=��a1+1����
��x������
��a1=1��
M1��1��1����
M2��a2��a 2������...
(4027��4027)
�����������������M1��a1��a 1����������y1=��x- a 1��2+a1�Ķ��㣬
������y=x2��������y1=��x- a 1��2+ a 1�ཻ��A1��
��x2=��x- a 1��2+ a 1��
��2a1x= a 12+ a 1��
x=��a1+1����
��x������
��a1=1��
M1��1��1����
M2��a2��a 2������...
�����ܶ϶���ABCΪ���������ε��ǣ� ��
A.��A=30�㣬��B=60�� B.��A=50�㣬��B=80��
C.AB=AC=2��BC=4 D.AB=3��BC=7���ܳ�Ϊ10
 B
��������
���������A��B���������ε��ڽǺ�����������ǣ��ɵý����C������������Σ�D�����ܳ�����������ɵõ��𰸣����ݵ��������ε��ж����������������ų��ķ����жϣ�
��������
A�������������ڽǺͶ����ã���C=180�㩁60�㩁30��=90�㣬�ʲ��ǵ��������Σ�
B�������������ڽǺͶ����ã���C=180�㩁50�㩁80��=50�㣬���ǵ��������Σ�
C������...
B
��������
���������A��B���������ε��ڽǺ�����������ǣ��ɵý����C������������Σ�D�����ܳ�����������ɵõ��𰸣����ݵ��������ε��ж����������������ų��ķ����жϣ�
��������
A�������������ڽǺͶ����ã���C=180�㩁60�㩁30��=90�㣬�ʲ��ǵ��������Σ�
B�������������ڽǺͶ����ã���C=180�㩁50�㩁80��=50�㣬���ǵ��������Σ�
C������... ij��˾����������ԭ����aԪ��������������������ﵽ��y��Ԫ�����ÿ�������İٷ�������x����ôy��x�ĺ�����ϵ�ǣ���
A. y=x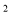 ��a B. y=a��x��1��
��a B. y=a��x��1��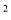 C. y=a��1��x��
C. y=a��1��x��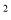 D. y=a��1��x��
D. y=a��1��x��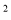
 D
��������������������������������һ��ͨ�ù�ʽ�ɵã�y=a.
D
��������������������������������һ��ͨ�ù�ʽ�ɵã�y=a. ���κ���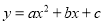 ��ͼ����ͼ��ʾ�������н��۳������ǣ� ��
��ͼ����ͼ��ʾ�������н��۳������ǣ� ��
A. a��0��bc��0������0 B. a��0��bc��0������0
C. a��0��bc��0������0 D. a��0��bc��0������0
 D
����������������
�������߿������£���a��0���߶Գ���x=����b��0����������y��Ľ�����x���Ϸ�����c��0����bc��0����������x�����������㣬�����0����ѡD��
D
����������������
�������߿������£���a��0���߶Գ���x=����b��0����������y��Ľ�����x���Ϸ�����c��0����bc��0����������x�����������㣬�����0����ѡD�� ��ͼ������ABCD�����߳�AB��18cm��AD��4cm.��P��Q�ֱ��A��Bͬʱ������P�ڱ�AB����AB������ÿ��2cm���ٶ������˶���Q�ڱ�BC����BC������ÿ��1cm���ٶ������˶������˶�ʱ��Ϊx�룬��PBQ�����Ϊy(cm2)��
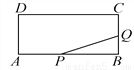
(1)��y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
(2)���PBQ����������ֵ��
 ��1��y����x2��9x(0��x��4)����2����PBQ����������ֵ��20cm2.
�������������������1���ֱ��ʾ��PB��BQ�ij���Ȼ����������ε������ʽ��ʽ�������ɵý⣻
��2���Ѻ�����ϵʽ�����ɶ���ʽ����ʽ��Ȼ����ݶ��κ�������ֵ������
�����������1����S��PBQ��PB��BQ��
PB��AB��AP��18��2x��
BQ��x��
��y�� (18��2x)x��...
��1��y����x2��9x(0��x��4)����2����PBQ����������ֵ��20cm2.
�������������������1���ֱ��ʾ��PB��BQ�ij���Ȼ����������ε������ʽ��ʽ�������ɵý⣻
��2���Ѻ�����ϵʽ�����ɶ���ʽ����ʽ��Ȼ����ݶ��κ�������ֵ������
�����������1����S��PBQ��PB��BQ��
PB��AB��AP��18��2x��
BQ��x��
��y�� (18��2x)x��... С����ɲ������s(m)���ٶ�v(km/h)֮��ĺ�����ϵʽΪs��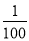 v2��һ��С�����ٶ�Ϊ100km/h����ǰ��80m��ͣ��һ�����ϳ�����ʱɲ��_______(��ᡱ���ᡱ)��Σ�գ�
v2��һ��С�����ٶ�Ϊ100km/h����ǰ��80m��ͣ��һ�����ϳ�����ʱɲ��_______(��ᡱ���ᡱ)��Σ�գ�
 ��
�����������������������Ѵ��뼴�����s��ֵ����80�Ƚϼ����ж�.
���У���ʱ��
���ʱɲ������Σ��.
��
�����������������������Ѵ��뼴�����s��ֵ����80�Ƚϼ����ж�.
���У���ʱ��
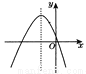
���ʱɲ������Σ��. ��֪���κ���y��ax2��bx��c��ͼ����ͼ��������������ȷ����( )
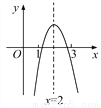
A. abc��0 B. ��3a��c��0
C. b2��4ac��0 D. ���ú���ͼ������ƽ��2����λ�����õ������ߵĽ���ʽΪy��ax2��c
 B
���������⣺A���ɿ������£��ɵ�a��0��������������y�ύ�ڸ����ᣬ�ɵ�c��0��Ȼ���ɶԳ�����y���Ҳ࣬�õ�b��a��ţ���ɵ�b��0���ʵ�abc��0���ʱ�ѡ�����
B������ͼ֪�Գ���Ϊֱ��x=2����=2����b=��4a���ٸ���ͼ��֪��x=1ʱ��y=a+b+c=a��4a+c=��3a+c��0���ʱ�ѡ����ȷ��
C������������x�����������㣬�ɵ�b2��4ac��0���ʱ�ѡ�����
...
B
���������⣺A���ɿ������£��ɵ�a��0��������������y�ύ�ڸ����ᣬ�ɵ�c��0��Ȼ���ɶԳ�����y���Ҳ࣬�õ�b��a��ţ���ɵ�b��0���ʵ�abc��0���ʱ�ѡ�����
B������ͼ֪�Գ���Ϊֱ��x=2����=2����b=��4a���ٸ���ͼ��֪��x=1ʱ��y=a+b+c=a��4a+c=��3a+c��0���ʱ�ѡ����ȷ��
C������������x�����������㣬�ɵ�b2��4ac��0���ʱ�ѡ�����
... ��ͼ��ij��ɽ�˶�Ա��Ӫ��A���½�Ϊ30���б��AB����ɽ��B�����AB��2000�ף�����ʵ��������________�ף�
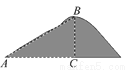
 1000
���������������������B��BC��ˮƽ���ڵ�C����Rt��ABC�У�����AB=200�ף���A=30�㣬���BC�ij��ȼ��ɣ�����B��BC��ˮƽ���ڵ�C����Rt��ABC�У���AB=2000�ף���A=30�㣬��BC=ABsin30��=2000��=1000
1000
���������������������B��BC��ˮƽ���ڵ�C����Rt��ABC�У�����AB=200�ף���A=30�㣬���BC�ij��ȼ��ɣ�����B��BC��ˮƽ���ڵ�C����Rt��ABC�У���AB=2000�ף���A=30�㣬��BC=ABsin30��=2000��=1000 �Ѷ���ʽ ��a��2��+m��2��a���ֽ���ʽ���ڣ� ��.
��a��2��+m��2��a���ֽ���ʽ���ڣ� ��.
A����a��2����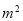 +m�� B����a��2����
+m�� B����a��2����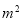 ��m��
��m��
C��m��a��2����m��1�� D��m��a��2����m+1��
 C��
��������
����������Ȱѣ�2��a��ת��Ϊ��a��2����Ȼ����ȡ����ʽm��a��2�����ɵã�a��2��+m��2��a��= m��a��2����m��1��.
��ѡ��C��
C��
��������
����������Ȱѣ�2��a��ת��Ϊ��a��2����Ȼ����ȡ����ʽm��a��2�����ɵã�a��2��+m��2��a��= m��a��2����m��1��.
��ѡ��C�� 
