题目内容
在二次函数y＝ax2＋bx＋c中，若a与c异号，则其图象与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
A
【解析】【解析】
∵a与c异号，∴ac＜0，∴△=＞0，∴二次函数图象与x轴的交点个数为2．故选A．
练习册系列答案
相关题目
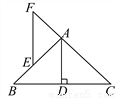
如图，在△ABC中，AB＝AC，AD⊥BC于D，E是AB上的一点，EF∥AD交CA的延长线于F.
求证：△AEF是等腰三角形．
见解析
【解析】试题分析：首先根据等腰三角形底边上的三线合一定理可得：AD为∠BAC的角平分线，根据平行线的性质得出∠F=∠CAD，∠FEA=∠BAD，从而∠FEA=∠F，得出等腰三角形．
试题解析：∵AB=AC，AD⊥BC， ∴∠BAD=∠CAD， 又∵AD∥EF，
∴∠F=∠CAD，∠FEA=∠BAD， ∴∠FEA=∠F， ∴△AEF是等腰三角形． 如图，隧道的截面是抛物线，可以用y=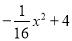 
表示，该隧道内设双行道，限高为3m，那么每条行道宽是（ ）
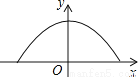
A. 不大于4m B. 恰好4m C. 不小于4m D. 大于4m，小于8m
A
【解析】把y=3代入y= 中得：
x=4，x= -4（舍去）．
∴每条行道宽应不大于4m．
故选A．
点睛；本题考查二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．由题意可知，直接把y=3代入解析式求解即可． 在体育测试时，初三的一名高个子男生推铅球，已知铅球所经过的路线是某二次函数图象的一部分(如图)，若这个男生出手处A点的坐标为(0，2)，铅球路线的最高处B点的坐标为B(6，5).
(1)求这个二次函数的表达式；
(2)该男生把铅球推出去多远?(精确到0.01米).
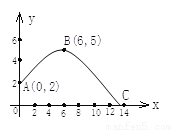
（1）y= (x-6)2+5；（2）该男生把铅球推出约13.75米
【解析】试题分析：（1）根据顶点坐标B(6,5)可设函数关系式为y=a(x-6)2+5，再把A(0,2)代入即可求得结果；
（2）把y=0代入求得图象与x轴的交点坐标，即可得到结果.
(1)设y=a(x-6)2+5,
则由A(0,2)得2=a(0-6)2+5，解得a=.
故y= (x-6)2+5；
... 不论m为何实数，抛物线y＝x2－mx＋m－2（ ）
A.在x轴上方 B.与x轴只有一个交点
C.与x轴有两个交点 D.在x轴下方
C
【解析】
试题分析：，当△=-4ac>0时，函数与x轴有两个交点；当△=-4ac=0时，函数与x轴有一个交点；当△=-4ac<0时，函数与x轴没有交点.根据题意可得：△=-4(m-2)=+4>0，则函数与x轴有两个交点. 某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系：
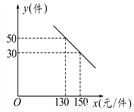
(1)求出y与x之间的函数关系式；
(2)写出每天的利润W与销售单价x之间的函数关系式；若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？
（1）y＝－x＋180；（2）售价定为140元/件时，每天最大利润W＝1600元．
【解析】（1）设y与x之间的函数关系式为y=kx+b（k≠0），根据所给函数图象列出关于kb的关系式，求出k、b的值即可；
（2）把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式，由此关系式即可得出结论．
【解析】
（1）设y与x之间的函数关系式为y=kx+b（k≠0），由所给... 开口向下的抛物线y＝(m2－2)x2＋2mx＋1的对称轴经过点(－1，3)，则m＝_____．
－1
【解析】由于抛物线y=（m2-2）x2+2mx+1的对称轴经过点（-1，3），
∴对称轴为直线x=-1，x==-1，
解得m1=-1，m2=2．
由于抛物线的开口向下，所以当m=2时，m2-2=2＞0，不合题意，应舍去，
∴m=-1．
故答案为：-1. 小明乘滑草车沿坡比为1：2.4的斜坡下滑130米，求他下降的高度
50米
【解析】试题分析：根据坡比可设BC=x，AC=2.4x，根据勾股定理得出AB=2.6x，根据AB的长度得出x的值，从而得出BC的值，即下降的高度．
试题解析：∵坡比为1：2.4， ∴BC：AC=1：2.4， 设BC=x，AC=2.4x，
则AB= ∵AB=130米， ∴x=50， 则BC=x=50（米）． 下列函数中属于一次函数的是( )，属于反比例函数的是( )，属于二次函数的是( )
A. y＝x(x＋1) B. xy＝1
C. y＝2x2－2(x＋1)2 D.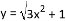 
CBA
【解析】根据题意可知y=x（x+1）=x2+x，可由二次函数的定义，可知是二次函数；根据xy=1是反比例关系，所以是反比例函数；而y＝2x2－2(x＋1)2= y＝2x2－2(x2+2x+1)=-4x-2，是一次函数；函数是带二次根号的函数.
故答案为：C、B、A.