如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（ ）
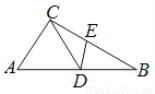
A. 50° B. 51° C. 51.5° D. 52.5°
D
【解析】试题分析：根据等腰三角形的性质推出∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，根据三角形的外角性质求出∠B=25°，由三角形的内角和定理求出∠BDE=∠BED=（180°﹣25°）=77.5°，，根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故答案选D． 若等腰三角形有两条边的长度为2和5，则此等腰三角形的周长为（ ）
A. 9 B. 12 C. 9或12 D. 10
B
【解析】由于等腰三角形的底边不确定，所以需要分类讨论，
①当底边长为2时，三边长为2，5，5，则周长为2+5+5=12；
②当底边长为5时，三边长为5，2，2，但5＞2+2，不能构成三角形.
故选B. 有下列命题说法：①锐角三角形中任何两个角的和大于90°；②等腰三角形一定是锐角三角形；③等腰三角形有一个外角等于120°，这个三角形一定是等边三角形；④等腰三角形中有一个是40°，那么它的底角是70°；⑤一个三角形中至少有一个角不小于60度．其中正确的有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
B
【解析】①中，必定正确．如果两个角的和不大于90°，则第三个内角将大于或等于90°，该三角形将不是锐角三角形；②中，这两个概念不能混淆，当等腰三角形的顶角是钝角时，该三角形是钝角三角形，故错误；③中，若等腰三角形有一个外角等于120°，则等腰三角形有一个内角等于60°，则这个三角形一定是等边三角形，故正确；④中，此题应分为两种情况，底角可以是40°或70°，故错误；⑤中，显然正确，如果都... 如图，已知DE∥BC，AB=AC，∠1=125°，则∠C的度数是（ ）
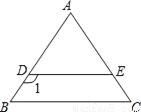
A. 55° B. 45° C. 35° D. 65°
A
【解析】∵∠1=125°，DE∥BC，∴∠B=180°–125°=55°，∵AB=AC，∴∠C=∠B=55°，故选A． 如图，已知等边△AEB和等边△BDC在线段AC同侧，则下面错误的是（ ）
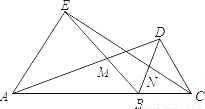
A. △ABD≌△EBC B. △NBC≌△MBD C. DM=DC D. ∠ABD=∠EBC
C
【解析】选项A，可以利用SAS验证，正确；选项B，可以利用AAS验证，正确；选项C，可证∠MBN=60°，若DM=DC=DB，则△DMB为等边三角形，即∠BDM=60°，∵∠EAB=∠DBC，∴AE∥BD．∴∠BDM=∠EAD=60°．与已知不符，错误；选项D，可由∠ABE，∠DBC同加一个∠DBE得到，正确.所以错误的是第三个,故选C. 如图，在等腰△ABC中，∠A=80°，∠B和∠C的平分线相交于点O
（1）连接OA，求∠OAC的度数；
（2）求：∠BOC。
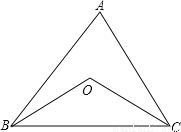
(1) 40°;(2) 130°
【解析】试题分析：（1）连接AO，利用等腰三角形的对称性即可求得∠OAC的度数；（2）利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系，再把∠A代入即可求∠BOC的度数．
试题解析：
（1）连接AO，
∵在等腰△ABC中，∠B和∠C的平分线相交于点O，
∴等腰△ABC关于线段AO所在的直线对称，
∵∠A=80°，
... 如图，在等腰三角形ABC中，AD、BE分别是底边BC和腰AC上的高线，DA、BE的延长线交于点P．若∠BAC=110°，求∠P的度数。
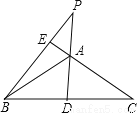
35°
【解析】试题分析：根据等腰三角形三线合一的性质可求得∠DAC的度数，根据对顶角相等求得∠EAP的度数，再由直角三角形的两锐角互余即可求得∠P的度数.
试题解析：
∵△ABC是等腰三角形，AB=AC，AD⊥BC，∠BAC=110°，
∴∠DAB=∠DAC=55°，
∵∠DAC=∠EAP（对顶角相等），
∴∠EAP=∠DAC=55°，
又∵BE是腰AC... 如图，已知△ABC中，AB=AC，周长为24，AC边上的中线BD把△ABC分成周长差为6的两个三角形，则△ABC各边的长分别为多少？
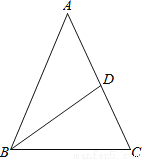
三角形的各边长为10、10、4
【解析】试题分析：分AB＞BC和AB＜BC两种情况求得AB、BC的长，再由三角形的三边关系进行取舍即可.
试题解析：
根据题意结合图形，分成两部分的周长的差等于腰长与底边的差，
（1）若AB＞BC，则AB-BC=6，
又因为2AB+BC=24，
联立方程组并求解得：AB=10，BC=4，
10、10、4三边能够组成三角形；
... 如图，在△ABC中，AB=AC，BF=CD，BD=CE，∠FDE=α，探索α与∠B的关系。
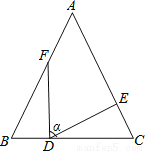
∠α=∠B，理由见解析
【解析】试题分析：根据已知条件易证△BFD≌△CDE，得出∠BFD=∠CDE，再由角之间的转化，进而可得出结论．
【解析过程】
试题解析：
∠α=∠B，理由为：
证明：∵AB=AC（已知），
∴∠B=∠C（等边对等角），
在△BDF和△CED中，
∴△BDF≌△CED（SAS），
∴∠BFD=∠CDE（全等三角形对应角相... 已知在△ABC中，AB=AC。
（1）若D为AC的中点，BD把三角形的周长分为24cm和30cm两部分，求△ABC三边的长；
（2）若D为AC上一点，试说明AC＞
（BD+DC）。
（1）三角形的三边长为16，16，22或20，20，14；（2）理由见解析
【解析】试题分析：（1）分两种情况讨论：当AB+AD=30，BC+DC=24或AB+AD=24，BC+DC=30，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为16，16，22或20，20，14；
（2）根据三角形两边之和大于第三边即可得到AC＞（BD+DC）.
试题解析：
（1）设三角形...