题目内容
有下列命题说法:①锐角三角形中任何两个角的和大于90°;②等腰三角形一定是锐角三角形;③等腰三角形有一个外角等于120°,这个三角形一定是等边三角形;④等腰三角形中有一个是40°,那么它的底角是70°;⑤一个三角形中至少有一个角不小于60度.其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】①中,必定正确.如果两个角的和不大于90°,则第三个内角将大于或等于90°,该三角形将不是锐角三角形;②中,这两个概念不能混淆,当等腰三角形的顶角是钝角时,该三角形是钝角三角形,故错误;③中,若等腰三角形有一个外角等于120°,则等腰三角形有一个内角等于60°,则这个三角形一定是等边三角形,故正确;④中,此题应分为两种情况,底角可以是40°或70°,故错误;⑤中,显然正确,如果都...
B
【解析】①中,必定正确.如果两个角的和不大于90°,则第三个内角将大于或等于90°,该三角形将不是锐角三角形;②中,这两个概念不能混淆,当等腰三角形的顶角是钝角时,该三角形是钝角三角形,故错误;③中,若等腰三角形有一个外角等于120°,则等腰三角形有一个内角等于60°,则这个三角形一定是等边三角形,故正确;④中,此题应分为两种情况,底角可以是40°或70°,故错误;⑤中,显然正确,如果都...
下列事件中,属于随机事件的是( )
A. 通常水加热到100℃时沸腾
B. 测量孝感某天的最低气温,结果为﹣150℃
C. 一个袋中装有5个黑球,从中摸出一个是黑球
D. 篮球队员在罚球线上投篮一次,未投中
 D
【解析】试题解析:结合所学的随机事件与必然事件的意义,A必然发生,是必然事件;B一定不会发生,是必然事件;C一定会发生,是必然事件;D 罚球投篮一次未投中是可能发生的,属于随机事件.故选D.
D
【解析】试题解析:结合所学的随机事件与必然事件的意义,A必然发生,是必然事件;B一定不会发生,是必然事件;C一定会发生,是必然事件;D 罚球投篮一次未投中是可能发生的,属于随机事件.故选D. 如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(﹣2,0),
B(4,0)与y轴交于点C.
(Ⅰ)求抛物线的解析式及其顶点D的坐标;
(Ⅱ)求△BCD的面积;
(Ⅲ)若直线CD交x轴与点E,过点B作x轴的垂线,交直线CD与点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).
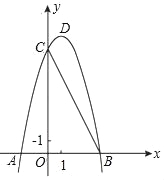
 (Ⅰ)抛物线的解析式:y=﹣x2+2x+8=﹣(x﹣1)2+9,顶点D(1,9);(Ⅱ)6;(Ⅲ)72.
【解析】
试题分析:(Ⅰ)利用待定系数法求出抛物线的解析式,通过对解析式进行配方能得到顶点D的坐标;
(Ⅱ)先求出直线BC解析式,进而用三角形的面积公式即可得出结论.
(Ⅲ)首先确定直线CD的解析式以及点E,F的坐标,若抛物线向上平移,首先表示出平移后的函数解析式;当x...
(Ⅰ)抛物线的解析式:y=﹣x2+2x+8=﹣(x﹣1)2+9,顶点D(1,9);(Ⅱ)6;(Ⅲ)72.
【解析】
试题分析:(Ⅰ)利用待定系数法求出抛物线的解析式,通过对解析式进行配方能得到顶点D的坐标;
(Ⅱ)先求出直线BC解析式,进而用三角形的面积公式即可得出结论.
(Ⅲ)首先确定直线CD的解析式以及点E,F的坐标,若抛物线向上平移,首先表示出平移后的函数解析式;当x... 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 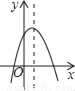 B.
B. 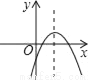 C.
C. 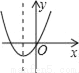 D.
D. 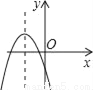
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?
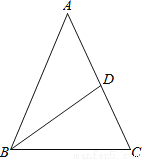
 三角形的各边长为10、10、4
【解析】试题分析:分AB>BC和AB<BC两种情况求得AB、BC的长,再由三角形的三边关系进行取舍即可.
试题解析:
根据题意结合图形,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=10,BC=4,
10、10、4三边能够组成三角形;
...
三角形的各边长为10、10、4
【解析】试题分析:分AB>BC和AB<BC两种情况求得AB、BC的长,再由三角形的三边关系进行取舍即可.
试题解析:
根据题意结合图形,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=10,BC=4,
10、10、4三边能够组成三角形;
... 已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹).
 见解析
【解析】试题分析:根据题意写出已知和求作,然后再画出图形即可.
试题解析:已知:线段a和∠α,如下图(1).
求作:Rt△ABC,使BC=a,∠C=90?,∠A=∠α.
作法:(1)作∠α的余角∠β.
(2)作∠MBN=∠β.
(3)在射线BM上截取BC=a.
(4)过点C作CA⊥BM,交BN于点A,如图(2).
△ABC就是所求的直角三角形...
见解析
【解析】试题分析:根据题意写出已知和求作,然后再画出图形即可.
试题解析:已知:线段a和∠α,如下图(1).
求作:Rt△ABC,使BC=a,∠C=90?,∠A=∠α.
作法:(1)作∠α的余角∠β.
(2)作∠MBN=∠β.
(3)在射线BM上截取BC=a.
(4)过点C作CA⊥BM,交BN于点A,如图(2).
△ABC就是所求的直角三角形... △ABC中,AB=5,BC=3,则中线BD的取值范围是_________.
 1<BD<4
【解析】延长BD到E,使BD=DE,连接AE,如图:
∵BD是△ABC中线,
∴AD=DC,
在△BDC和△EDA中,
∵,
∴△BDC≌△EDA.
∴BC=AE=3,
∵在△ABE中,根据三角形的三边关系定理得:5+3>BE>5-3,
∴2<2BD<8,
即1<BD<4.
故答案为:1<BD<4.
1<BD<4
【解析】延长BD到E,使BD=DE,连接AE,如图:
∵BD是△ABC中线,
∴AD=DC,
在△BDC和△EDA中,
∵,
∴△BDC≌△EDA.
∴BC=AE=3,
∵在△ABE中,根据三角形的三边关系定理得:5+3>BE>5-3,
∴2<2BD<8,
即1<BD<4.
故答案为:1<BD<4. 已知a+b=3,ab=2,求代数式a3b+2a2b2+ab3的值.
 18
【解析】试题分析:先提取公因式ab,再根据完全平方公式进行二次分解,然后代入数据进行计算即可得解.
【解析】
a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2,
将a+b=3,ab=2代入得,ab(a+b)2=2×32=18.
故代数式a3b+2a2b2+ab3的值是18.
18
【解析】试题分析:先提取公因式ab,再根据完全平方公式进行二次分解,然后代入数据进行计算即可得解.
【解析】
a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2,
将a+b=3,ab=2代入得,ab(a+b)2=2×32=18.
故代数式a3b+2a2b2+ab3的值是18. 在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.
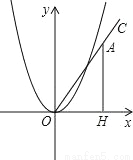
 【解析】试题解析:①如图1,当∠POQ=∠OAH=30°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
∵∠AOH=60°,
∴直线OA:y=x,
联立抛物线的解析式得: ,
解得: 或,
故A(,3);
②当∠POQ=∠AOH=60°,此时△POQ≌△AOH,
易知∠POH=30°,则直线y=x,联立抛物线的解析式,得: ,
解得:...
【解析】试题解析:①如图1,当∠POQ=∠OAH=30°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
∵∠AOH=60°,
∴直线OA:y=x,
联立抛物线的解析式得: ,
解得: 或,
故A(,3);
②当∠POQ=∠AOH=60°,此时△POQ≌△AOH,
易知∠POH=30°,则直线y=x,联立抛物线的解析式,得: ,
解得:... 
