��Ŀ����
��֪�ڡ�ABC�У�AB=AC��

��1����DΪAC���е㣬BD�������ε��ܳ���Ϊ24cm��30cm�����֣����ABC���ߵij���
��2����DΪAC��һ�㣬��˵��AC�� ��BD+DC����
��BD+DC����
 ��1�������ε����߳�Ϊ16��16��22��20��20��14����2�����ɼ�����
�������������������1��������������ۣ���AB+AD=30��BC+DC=24��AB+AD=24��BC+DC=30�����Ը��ݵ��������ε�������Ⱥ����ߵ����ʿ���ã����߳�Ϊ16��16��22��20��20��14��
��2����������������֮�ʹ��ڵ������ɵõ�AC����BD+DC��.
���������
��1����������...
��1�������ε����߳�Ϊ16��16��22��20��20��14����2�����ɼ�����
�������������������1��������������ۣ���AB+AD=30��BC+DC=24��AB+AD=24��BC+DC=30�����Ը��ݵ��������ε�������Ⱥ����ߵ����ʿ���ã����߳�Ϊ16��16��22��20��20��14��
��2����������������֮�ʹ��ڵ������ɵõ�AC����BD+DC��.
���������
��1����������...
�����¼�Ϊ��Ȼ�¼����ǣ�������
A. С���μӱ�����ѧ���ԣ��ɼ���150��
B. ij����˶�Ա���һ�Σ����а���
C. ���ӻ���CCTV��һ��Ŀ���ڲ�������
D. �ڴ���װ��2�������1������������2�������б��к���
 D
�����������������A��С���μӱ�����ѧ���ԣ��ɼ���150��������¼�����Aѡ�����
B��ij����˶�Ա���һ�Σ����а���������¼�����Bѡ�����
C�����ӻ�������һ��Ŀ���ڲ�������������¼�����Cѡ�����
D���ڴ���װ�����������һ���������������������б��к����DZ�Ȼ�¼�����Dѡ����ȷ��
��ѡD��
D
�����������������A��С���μӱ�����ѧ���ԣ��ɼ���150��������¼�����Aѡ�����
B��ij����˶�Ա���һ�Σ����а���������¼�����Bѡ�����
C�����ӻ�������һ��Ŀ���ڲ�������������¼�����Cѡ�����
D���ڴ���װ�����������һ���������������������б��к����DZ�Ȼ�¼�����Dѡ����ȷ��
��ѡD�� ����A(3��2)��x������ƽ��4����λ���ȵõ���A�䣬���A�����ԭ��ԳƵĵ��������( )
A. (-3��2) B. (-1��2) C. (1��2) D. (1��-2)
 D
���������������������A��3��2������ƽ��4����λ���ȵõ�A�䣬�ɵõ�A�������Ϊ����1��2�������Ե�A�����y��ԳƵĵ�������ǣ�1��2������ѡD��
D
���������������������A��3��2������ƽ��4����λ���ȵõ�A�䣬�ɵõ�A�������Ϊ����1��2�������Ե�A�����y��ԳƵĵ�������ǣ�1��2������ѡD�� ���κ���y=x2��2x+6����Сֵ��____��
 5
�����������������y=x2��2x+6=x2��2x+1+5
=��x��1��2+5��
�ɼ������κ�������СֵΪ5��
5
�����������������y=x2��2x+6=x2��2x+1+5
=��x��1��2+5��
�ɼ������κ�������СֵΪ5�� ��ͼ����a��0��b��0��c��0����������y=ax2+bx+c�Ĵ���ͼ��Ϊ��������
A. 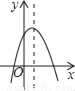 B.
B. 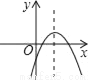 C.
C. 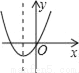 D.
D. 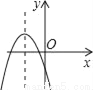
 B
�������������������a��0��
�������ߵĿ��ڷ������£�
�ʵ�����ѡ�����
��c��0��
����������y��Ľ���Ϊ��y��ĸ������ϣ�
�ʵ�һ��ѡ�����
��a��0��b��0���Գ���Ϊx=��0��
��Գ�����y���Ҳ࣬
�ʵ��ĸ�ѡ�����
��ѡB��
B
�������������������a��0��
�������ߵĿ��ڷ������£�
�ʵ�����ѡ�����
��c��0��
����������y��Ľ���Ϊ��y��ĸ������ϣ�
�ʵ�һ��ѡ�����
��a��0��b��0���Գ���Ϊx=��0��
��Գ�����y���Ҳ࣬
�ʵ��ĸ�ѡ�����
��ѡB�� ��ͼ����֪�ȱߡ�AEB�͵ȱߡ�BDC���߶�ACͬ�࣬�����������ǣ�������
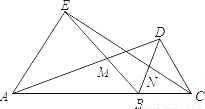
A. ��ABD�ա�EBC B. ��NBC�ա�MBD C. DM=DC D. ��ABD=��EBC
 C
��������ѡ��A����������SAS��֤����ȷ��ѡ��B����������AAS��֤����ȷ��ѡ��C����֤��MBN=60�㣬��DM=DC=DB�����DMBΪ�ȱ������Σ�����BDM=60�㣬�ߡ�EAB=��DBC����AE��BD�����BDM=��EAD=60�㣮����֪����������ѡ��D�����ɡ�ABE����DBCͬ��һ����DBE�õ�����ȷ.���Դ�����ǵ�����,��ѡC.
C
��������ѡ��A����������SAS��֤����ȷ��ѡ��B����������AAS��֤����ȷ��ѡ��C����֤��MBN=60�㣬��DM=DC=DB�����DMBΪ�ȱ������Σ�����BDM=60�㣬�ߡ�EAB=��DBC����AE��BD�����BDM=��EAD=60�㣮����֪����������ѡ��D�����ɡ�ABE����DBCͬ��һ����DBE�õ�����ȷ.���Դ�����ǵ�����,��ѡC. ��֪һֱ�DZߺ�����ֱ�DZߵĶԽǣ�����ֱ��������(�ó߹���ͼ����д��������Ҫ������ͼ�ۼ�)��
 ������
�������������������������д����֪��������Ȼ���ٻ���ͼ�μ��ɣ�
�����������֪���߶�a�͡Ϧ�������ͼ(1).
������Rt��ABC��ʹBC=a����C=90?����A=�Ϧ�.
������(1)���Ϧ�����ǡϦ�.
(2)����MBN=�Ϧ�.
(3)������BM�Ͻ�ȡBC=a.
(4)����C��CA��BM����BN�ڵ�A����ͼ(2).
��ABC���������ֱ��������...
������
�������������������������д����֪��������Ȼ���ٻ���ͼ�μ��ɣ�
�����������֪���߶�a�͡Ϧ�������ͼ(1).
������Rt��ABC��ʹBC=a����C=90?����A=�Ϧ�.
������(1)���Ϧ�����ǡϦ�.
(2)����MBN=�Ϧ�.
(3)������BM�Ͻ�ȡBC=a.
(4)����C��CA��BM����BN�ڵ�A����ͼ(2).
��ABC���������ֱ��������... ����������һ�㣬�������ߵľ�����ȣ�������Ǹ������ε�(����)
A. �������߽��� B. ������ƽ���߽���
C. �������߽��� D. ������������ֱ�߽���
 B
�����������������ν�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȿɵô˵�Ϊ��ƽ���ߵĽ���.
��ѡ��B.
B
�����������������ν�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȿɵô˵�Ϊ��ƽ���ߵĽ���.
��ѡ��B. ����������y=2x2����ƽ��3����λ�����������ߵĽ���ʽΪ�� ��
A��y=2x2+3 B��y=2x2��3 C��y=2��x��3��2 D��y=2��x+3��2
 A��
��������
����������ɡ��ϼ��¼�����ԭ���֪�������κ���y=2x2����ƽ��3����λ�ɵõ�����y=2x2+3��
��ѡ��A��
A��
��������
����������ɡ��ϼ��¼�����ԭ���֪�������κ���y=2x2����ƽ��3����λ�ɵõ�����y=2x2+3��
��ѡ��A�� 
