题目内容
若等腰三角形有两条边的长度为2和5，则此等腰三角形的周长为（ ）
A. 9 B. 12 C. 9或12 D. 10
B
【解析】由于等腰三角形的底边不确定，所以需要分类讨论，
①当底边长为2时，三边长为2，5，5，则周长为2+5+5=12；
②当底边长为5时，三边长为5，2，2，但5＞2+2，不能构成三角形.
故选B.
练习册系列答案
相关题目
有两个事件，事件A：367人中至少有2人生日相同；事件B：抛掷一枚均匀的骰子，朝上的面点数为偶数．下列说法正确的是（ ）
A. 事件A、B都是随机事件 B. 事件A、B都是必然事件
C. 事件A是随机事件，事件B是必然事件 D. 事件A是必然事件，事件B是随机事件
D
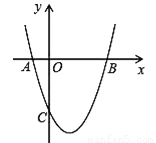
【解析】事件A、一年最多有366天，所以367人中必有2人的生日相同，是必然事件；事件B、抛掷一枚均匀的骰子，朝上的面点数为1、2、3、4、5、6共6种情况，点数为偶数是随机事件． 如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．
（1）y=x2﹣2x﹣3；（2）抛物线的对称轴x=1，顶点坐标（1，﹣4）；（3）（，4）或（，4）或（1，﹣4）．
【解析】试题分析：（1）由于抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3，然后利用根与系数即可确定b、c的值．
（2）根据S△PAB=8，求得P的纵坐标，把纵坐标代入抛物线的解析式即可求得... 关于二次函数y=x2﹣2x﹣3的图象，下列说法中错误的是（ ）
A. 当x＜2，y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是（0，﹣3）
A
【解析】试题分析：∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线开口向上，对称轴为x=1，当x＜1时y随x的增大而减小，故B、C正确，A不正确，
令x=0可得y=﹣3，
∴抛物线与y轴的交点坐标为（0，﹣3），故D正确，
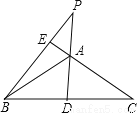
故选A． 如图，在等腰三角形ABC中，AD、BE分别是底边BC和腰AC上的高线，DA、BE的延长线交于点P．若∠BAC=110°，求∠P的度数。
35°
【解析】试题分析：根据等腰三角形三线合一的性质可求得∠DAC的度数，根据对顶角相等求得∠EAP的度数，再由直角三角形的两锐角互余即可求得∠P的度数.
试题解析：
∵△ABC是等腰三角形，AB=AC，AD⊥BC，∠BAC=110°，
∴∠DAB=∠DAC=55°，
∵∠DAC=∠EAP（对顶角相等），
∴∠EAP=∠DAC=55°，
又∵BE是腰AC... 已知：如图，在△ABC中有D、E两点，求证：BD＋DE＋EC＜AB＋AC．
见解析
【解析】试题分析：延长BD交AC于M点，延长CE交BD的延长线于点N．在△ABM中，AB+AM>BM，在△CNM中，NM+MC>NC，所以AB+AM+NM+MC>BM+NC，再由AM+MC=AC，BM=BN+NM可知AB+AC+NM>BN+NM+NC，故AB+AC>BN+NC，在△BNC中，BN+NC=BD+DN+NE+EC，在△DNE中，DN+NE>DE，由此即可得出结论．
... 三角形的一边上有一点，它到三个顶点的距离相等，则这个三角形是_______三角形．
直角
【解析】∵直角三角形斜边上的中线等于斜边的一半，
∴这个三角形是直角三角形.
故答案为：直角. 如图，在一块边长为a的正方形纸板四周，各剪去一个边长为b(b＜0)的正方形．
(1)用代数式表示阴影部分的面积；
(2)利用因式分解的方法计算当a＝15.4，b＝3.7时，阴影部分的面积．
(1) a2－4b²;(2) 182.4.
【解析】试题分析：
试题解析：（1）用大正方形的面积减去四个小正方形的面积即可求得阴影部分的面积；（2）把所得的代数式用平方差公式因式分解后，代入求值即可.
(1)S阴影＝a2－4b2；
(2)S阴影＝(a＋2b)(a－2b)＝(15.4＋2×3.7)(15.4－2×3.7)＝22.8×8＝182.4. 二次函数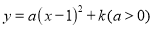
中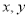
的几组对应值如下表．
| -2 | 1 | 5 |
| m | n | p |
表中m、n、p的大小关系为________________（用“＜”连接）
n＜m＜p
【解析】【解析】
设（-2，m）关于对称轴的对称点为（x，m）．∵二次函数的对称轴为x=1，∴ ，解得：x=4．∵a＞0，∴抛物线开口向上，在对称轴右侧，y随x的增大而增大．∵1＜4＜5，∴n＜m＜p．故答案为：n＜m＜p．