��Ŀ����
��ͼ���ڡ�ABC�У�AB=AC��BF=CD��BD=CE����FDE=����̽�������B�Ĺ�ϵ��
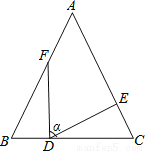
 �Ϧ�=��B�����ɼ�����
�����������������������֪������֤��BFD�ա�CDE���ó���BFD=��CDE�����ɽ�֮���ת���������ɵó����ۣ�
���������̡�
���������
�Ϧ�=��B������Ϊ��
֤������AB=AC����֪����
���B=��C���ȱ߶ԵȽǣ���
�ڡ�BDF�͡�CED�У�
���BDF�ա�CED��SAS����
���BFD=��CDE��ȫ�������ζ�Ӧ����...
�Ϧ�=��B�����ɼ�����
�����������������������֪������֤��BFD�ա�CDE���ó���BFD=��CDE�����ɽ�֮���ת���������ɵó����ۣ�
���������̡�
���������
�Ϧ�=��B������Ϊ��
֤������AB=AC����֪����
���B=��C���ȱ߶ԵȽǣ���
�ڡ�BDF�͡�CED�У�
���BDF�ա�CED��SAS����
���BFD=��CDE��ȫ�������ζ�Ӧ����...
 �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д��ӱ�ŷֱ�Ϊ1��2��3��4��5��5�ſ�Ƭ�У������ȡ1�ţ������¼��У���Ȼ�¼��ǣ�������
A. ���С��6 B. ��Ŵ���6 C. ��������� D. �����3
 A
��������������������С��6�DZ�Ȼ�¼�����Ŵ���6�Dz������¼��������������������¼��������3���¼�������¼�.
��ѡ��A
A
��������������������С��6�DZ�Ȼ�¼�����Ŵ���6�Dz������¼��������������������¼��������3���¼�������¼�.
��ѡ��A ��ͼ����ABC�͡�BDE�ǵȱ������Σ���A��B��D��һ��ֱ���ϣ�����AB=BD����һ�������α任����һ�������Σ�������
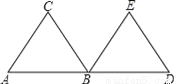
A. ������ƽ�Ƶõ�
B. ��������ת�õ�
C. ������ƽ�Ƶõ���Ҳ������ת�õ�
D. �Ȳ�����ƽ�Ƶõ���Ҳ��������ת�õ�
 C
����������������
�ߡ�ABC�͡�BDE�ǵȱ������Σ���A��B��D��һ��ֱ���ϣ�����AB=BD��
��������ȫ���������е�һ��������������һ���������Ƶ�B��ת90���õ�����۵õ��ģ���ѡC��
C
����������������
�ߡ�ABC�͡�BDE�ǵȱ������Σ���A��B��D��һ��ֱ���ϣ�����AB=BD��
��������ȫ���������е�һ��������������һ���������Ƶ�B��ת90���õ�����۵õ��ģ���ѡC�� ��֪�����ߺ�ֱ��l��ͬһֱ������ϵ�е�ͼ����ͼ��ʾ�������ߵĶԳ���Ϊֱ��x=��1��P1��x1��y1����P2��x2��y2�����������ϵĵ㣬P3��x3��y3����ֱ��l�ϵĵ㣬�ҩ�1��x1��x2��x3����1����y1��y2��y3�Ĵ�С��ϵΪ��������
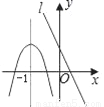
A. y1��y2��y3 B. y3��y1��y2 C. y3��y2��y1 D. y2��y1��y3
 D
���������������Գ���Ϊֱ��x=��1���ҩ�1��x1��x2����x����1ʱ��y2��y1��
����Ϊx3����1����һ�κ�����ͼ���֪����ʱ��P3��x3��y3���ڶ��κ���ͼ���Ϸ���
����y2��y1��y3��
��ѡ��D��
D
���������������Գ���Ϊֱ��x=��1���ҩ�1��x1��x2����x����1ʱ��y2��y1��
����Ϊx3����1����һ�κ�����ͼ���֪����ʱ��P3��x3��y3���ڶ��κ���ͼ���Ϸ���
����y2��y1��y3��
��ѡ��D�� ���ڶ��κ���y=x2��2x��3��ͼ������˵���д�����ǣ� ��
A. ��x��2��y��x���������С B. �����ĶԳ�����ֱ��x=1
C. �����Ŀ��ڷ������� D. ����ͼ����y��Ľ��������ǣ�0����3��
 A
�������������������y=x2��2x��3=��x��1��2��4��
�������߿������ϣ��Գ���Ϊx=1����x��1ʱy��x���������С����B��C��ȷ��A����ȷ��
��x=0�ɵ�y=��3��
����������y��Ľ�������Ϊ��0����3������D��ȷ��
��ѡA��
A
�������������������y=x2��2x��3=��x��1��2��4��
�������߿������ϣ��Գ���Ϊx=1����x��1ʱy��x���������С����B��C��ȷ��A����ȷ��
��x=0�ɵ�y=��3��
����������y��Ľ�������Ϊ��0����3������D��ȷ��
��ѡA�� ��ͼ����֪DE��BC��AB=AC����1=125�㣬���C�Ķ����ǣ�������
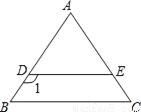
A. 55�� B. 45�� C. 35�� D. 65��
 A
���������ߡ�1=125�㣬DE��BC�����B=180��C125��=55�㣬��AB=AC�����C=��B=55�㣬��ѡA��
A
���������ߡ�1=125�㣬DE��BC�����B=180��C125��=55�㣬��AB=AC�����C=��B=55�㣬��ѡA�� ��֪����ͼ���ڡ�ABC����D��E���㣬��֤��BD��DE��EC��AB��AC��

 ������
������������������ӳ�BD��AC��M�㣬�ӳ�CE��BD���ӳ����ڵ�N���ڡ�ABM�У�AB+AM>BM���ڡ�CNM�У�NM+MC>NC������AB+AM+NM+MC>BM+NC������AM+MC=AC��BM=BN+NM��֪AB+AC+NM>BN+NM+NC����AB+AC>BN+NC���ڡ�BNC�У�BN+NC=BD+DN+NE+EC���ڡ�DNE�У�DN+NE>DE���ɴ˼��ɵó����ۣ�
...
������
������������������ӳ�BD��AC��M�㣬�ӳ�CE��BD���ӳ����ڵ�N���ڡ�ABM�У�AB+AM>BM���ڡ�CNM�У�NM+MC>NC������AB+AM+NM+MC>BM+NC������AM+MC=AC��BM=BN+NM��֪AB+AC+NM>BN+NM+NC����AB+AC>BN+NC���ڡ�BNC�У�BN+NC=BD+DN+NE+EC���ڡ�DNE�У�DN+NE>DE���ɴ˼��ɵó����ۣ�
... ��֪��ABC�������ڽǡ�A����B����C�����ϵʽ��B+��C=��A����������Σ�������
A. һ����һ���ڽ�Ϊ45�� B. һ����һ���ڽ�Ϊ60��
C. һ����ֱ�������� D. һ���Ƕ۽�������
 C
������������������ߡ�A+��B+��C=180�㣬��B+��C=��A��
��2��A=180�㣬
���A=90�㣬
����ABCһ����ֱ�������Σ�
��ѡC��
C
������������������ߡ�A+��B+��C=180�㣬��B+��C=��A��
��2��A=180�㣬
���A=90�㣬
����ABCһ����ֱ�������Σ�
��ѡC�� ��֪���κ���y=2x2+bx��1��
��1����֤������bȡʲôֵ�����κ���y=2x2+bx��1ͼ����x������������㣮
��2��������P����3��m����Q��1��m���ڸú���ͼ���ϣ�
����b��m��ֵ��
�ڽ����κ���ͼ������ƽ�ƶ��ٵ�λ���Ⱥõ��ĺ���ͼ����x��ֻ��һ�������㣿
 ��1������bȡʲôֵ�����κ���y=2x2+bx��1ͼ����x������������㣮
��2��b=4��m=5����3�����κ���ͼ������ƽ��3����λ
��������
�����������1���ȼ����б�ʽ��ֵ�������÷Ǹ��������ʿ��жϡ�=��0��Ȼ������б�ʽ��������ж���������x������������㣻
��2���������������ߵĶԳ��Կ�ȷ�������ߵĶԳ��᷽�̣��Ӷ������b��ֵ��Ȼ������Ա���Ϊ1����Ӧ�ĺ���ֵ���ɵ�...
��1������bȡʲôֵ�����κ���y=2x2+bx��1ͼ����x������������㣮
��2��b=4��m=5����3�����κ���ͼ������ƽ��3����λ
��������
�����������1���ȼ����б�ʽ��ֵ�������÷Ǹ��������ʿ��жϡ�=��0��Ȼ������б�ʽ��������ж���������x������������㣻
��2���������������ߵĶԳ��Կ�ȷ�������ߵĶԳ��᷽�̣��Ӷ������b��ֵ��Ȼ������Ա���Ϊ1����Ӧ�ĺ���ֵ���ɵ�... 
