题目内容
如图，已知等边△AEB和等边△BDC在线段AC同侧，则下面错误的是（ ）
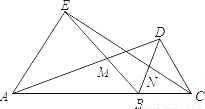
A. △ABD≌△EBC B. △NBC≌△MBD C. DM=DC D. ∠ABD=∠EBC
C
【解析】选项A，可以利用SAS验证，正确；选项B，可以利用AAS验证，正确；选项C，可证∠MBN=60°，若DM=DC=DB，则△DMB为等边三角形，即∠BDM=60°，∵∠EAB=∠DBC，∴AE∥BD．∴∠BDM=∠EAD=60°．与已知不符，错误；选项D，可由∠ABE，∠DBC同加一个∠DBE得到，正确.所以错误的是第三个,故选C.
轻松夺冠全能掌控卷系列答案下列成语所描述的事件是必然发生的是（ ）
A. 水中捞月 B. 拔苗助长 C. 守株待兔 D. 瓮中捉鳖
D
【解析】试题分析：必然事件是指一定会发生的事件；不可能事件是指不可能发生的事件；随机事件是指可能发生也可能不发生的事件。根据定义，对每个选项逐一判断A选项，不可能事件 B选项，不可能事件 C选项，随机事件D选项，必然事件 如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=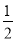
x刻画．
（1）请用配方法求二次函数图象的最高点P的坐标；
（2）小球的落点是A，求点A的坐标；
（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；
（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．
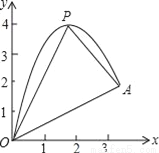
（1）最高点P的坐标为（2，4）；（2）点A的坐标为（， ）；（3）；（4）点M的坐标为（， ）
【解析】试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；
（2）联立两解析式，可求出交点A的坐标；
（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；
（4）过P... 抛物线y=x2﹣2x﹣3的图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=x2+bx+c，则b、c的值为（ ）
A．b=2，c=2 B．b=2，c=﹣1 C．b=﹣2，c=﹣1 D．b=﹣3，c=2
B．
【解析】
试题分析：y=x2﹣2x﹣3=x2﹣2x+1﹣4=（x﹣1）2﹣4，
图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=（x﹣1+2）2﹣4+2=（x+1）2﹣2=x2+2x﹣1，
则b=2，c=﹣1，
故选B． 已知在△ABC中，AB=AC。
（1）若D为AC的中点，BD把三角形的周长分为24cm和30cm两部分，求△ABC三边的长；
（2）若D为AC上一点，试说明AC＞
（BD+DC）。
（1）三角形的三边长为16，16，22或20，20，14；（2）理由见解析
【解析】试题分析：（1）分两种情况讨论：当AB+AD=30，BC+DC=24或AB+AD=24，BC+DC=30，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为16，16，22或20，20，14；
（2）根据三角形两边之和大于第三边即可得到AC＞（BD+DC）.
试题解析：
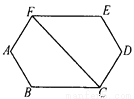
（1）设三角形... 已知：如图，AB＝DE，CD＝FA，∠A＝∠D，∠AFC＝∠DCF，则BC＝EF．你能说出它们相等的理由吗?
见解析
【解析】试题分析：首先连接CE、BF，然后根据条件可证明△ABF≌△DEC，再根据全等三角形的性质可得∠3=∠4，BF=EC，然后证明△BCF≌△EFC可得BC=EF．
试题解析：连接CE、BF，如图：
在△ABF和△DEC中， ，
∴△ABF≌△DEC(SAS)，
∴∠3=∠4，BF=EC，
∵∠AFC=∠DCF，
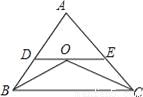
∴∠AFC?∠3=∠DCF?∠... 已知：如图，△ABC中，BO，CO分别是∠ABC和∠ACB的平分线，过O点的直线分别交AB、AC于点D、E，且DE∥BC．若AB=6cm，AC=8cm，则△ADE的周长为__．
14cm
【解析】两直线平行，内错角相等，以及根据角平分线性质，可得△OBD、△EOC均为等腰三角形，由此把△AEF的周长转化为AC+AB．
【解析】
∵DE∥BC，∴∠DOB=∠OBC，又∵BO是∠ABC的角平分线，∴∠DBO=∠OBC，∴∠DBO=∠DOB，∴BD=OD，同理：OE=EC，
∴△ADE的周长=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c... 下列长度的各组线段中，能组成三角形的是 ( )
A. 4、5、6 B. 6、8、15 C. 5、7、12 D. 3、9、13
A
【解析】根据三角形的三边关系，得
A.4+5>6，能组成三角形，符合题意；
B.6+8<15，不能够组成三角形，不符合题意；
C.5+7=12，不能够组成三角形，不符合题意；
D.3+7<13，不能够组成三角形，不符合题意。
故选：A. 如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8s时，离地面的高度为3.5m.
(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？
（1）足球飞行的时间是s时，足球离地面最高，最大高度是4.5m；（2）能.
【解析】试题分析：（1）由题意得：函数y=at2+5t+c的图象经过（0，0.5）（0.8，3.5），于是得到，求得抛物线的解析式为：y=﹣t2+5t+，当t=时，y最大=4.5；
（2）把x=28代入x=10t得t=2.8，当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，于是得到他能将球直...