题目内容
如图，已知DE∥BC，AB=AC，∠1=125°，则∠C的度数是（ ）
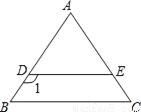
A. 55° B. 45° C. 35° D. 65°
A
【解析】∵∠1=125°，DE∥BC，∴∠B=180°–125°=55°，∵AB=AC，∴∠C=∠B=55°，故选A．
下列事件中，属于必然事件的是（ ）
A. 打开电视，正在播放《新闻联播》 B. 抛掷一次硬币正面朝上
C. 袋中有3个红球，从中摸出一球是红球 D. 阴天一定下雨
C
【解析】试题解析：A．打开电视，正在播放《新闻联播》是随机事件，因为也可能播放其它内容；
B．抛掷一次硬币正面朝上是随机事件，也可能反面朝上；
C. 袋中有3个红球，从中摸出一球是红球，是必然事件，因为袋子中只有红球，无论怎么摸，只能摸出红球；
D．阴天一定下雨是随机事件，也可能只阴天不下雨.
故选C. 如图，已知正方形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，抛物线y=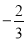
x2+bx+c经过点A，B，交正x轴于点D，E是OC上的动点（不与C重合）连接EB，过B点作BF⊥BE交y轴与F
（1）求b，c的值及D点的坐标；
（2）求点E在OC上运动时，四边形OEBF的面积有怎样的规律性？并证明你的结论；
（3）连接EF，BD，设OE=m，△BEF与△BED的面积之差为S，问：当m为何值时S最小，并求出这个最小值．
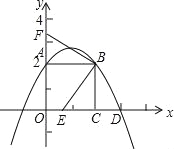
（1）b=，c=2；D点坐标为（3，0）．（2）点E在OC上运动时，四边形OEBF的面积不变；（3）当m=2﹣时S最小为0．
【解析】
试题分析：（1）把点A，B代入抛物线y=x2+bx+c求得b、c即可，y=0，建立方程求得点D；
（2）四边形OEBF的面积不变，利用三角形全等证得结论即可；
（3）用m分别表示出两个三角形的面积，求差探讨得出答案即可．
试题解析：（... 如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
A. a=﹣1 B. a=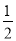
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
故选C． 如图，在△ABC中，AB=AC，BF=CD，BD=CE，∠FDE=α，探索α与∠B的关系。
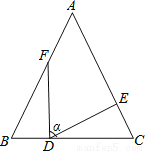
∠α=∠B，理由见解析
【解析】试题分析：根据已知条件易证△BFD≌△CDE，得出∠BFD=∠CDE，再由角之间的转化，进而可得出结论．
【解析过程】
试题解析：
∠α=∠B，理由为：
证明：∵AB=AC（已知），
∴∠B=∠C（等边对等角），
在△BDF和△CED中，
∴△BDF≌△CED（SAS），
∴∠BFD=∠CDE（全等三角形对应角相... 已知：如图，点C在线段AB上，以AC和BC为边在AB的同侧作正三角形△ACM和△BCN，连结AN、BM，分别交CM、CN于点P、Q．求证：PQ∥AB．
见解析
【解析】试题分析：首先证明△ACN≌△MCB可得∠ANC=∠MBC，再证明△PCN≌△QCB可得PC=QC，再有∠MCN=60°可得△PCQ是等边三角形，进而得到∠PQC=60°，可证明PQ∥AB．
试题解析：∵△ACM和△BCN都是正三角形，
∴∠ACM=∠BCN=60°，AC=CM，BC=CN.
∵点C在线段AB上，
∴∠ACM=∠BCN=∠MCN=60°... 如图，△ABC中，∠C＝90°，CD⊥AB，CM平分AB，CE平分∠DCM，则∠ACE的度数是______．
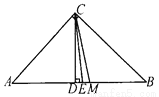
45°
【解析】∵△ABC中,∠C=90°，
∴∠A+∠B=90°，
∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠ACD=∠B，
∵CM平分AB，
∴AM=BM=CM，
∴∠BCM=∠B，
∴∠BCM=∠ACD，
∵CE平分∠DCM，
∴∠DCE=∠MCE，
∴∠ACD+∠DCE=∠BCM+∠M... 一个钝角三角形的三条角平分线所在的直线一定交于一点，这交点一定在( )
A. 三角形内部 B. 三角形的一边上 C. 三角形外部 D. 三角形的某个顶点上
A
【解析】三角形三条角平分线所在的直线一定交于一点，这一点是三角形的内心即内切圆的圆心，此点在三角形（锐角三角形、直角三角形、钝角三角形）内部.
故选：A. 已知抛物线y=ax2+bx+3的对称轴是直线x=1．
（1）求证：2a+b=0；
（2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．
（1）见解析；（2）x=－2
【解析】试题分析：直接利用对称轴公式代入求出即可；根据（1）中所求，再将x=4代入方程求出a，b的值，进而解方程得出即可．
试题解析：（1）证明：∵对称轴是直线x=1=﹣，∴b=－2a ∴2a+b=0；
（2）∵ax2+bx﹣8=0的一个根为4，∴16a+4b﹣8=0，∵b=﹣2a，∴16a﹣8a﹣8=0，
解得：a=1，则b=﹣2，∴a+bx...