��Ŀ����
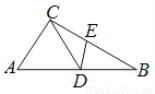
��ͼ����ABC�У�DΪAB��һ�㣬EΪBC��һ�㣬��AC=CD=BD=BE����A=50�㣬���CDE�Ķ���Ϊ�� ��
A. 50�� B. 51�� C. 51.5�� D. 52.5��
 D
��������������������ݵ��������ε������Ƴ���A=��CDA=50�㣬��B=��DCB����BDE=��BED�����������ε�������������B=25�㣬�������ε��ڽǺͶ��������BDE=��BED=��180�㩁25�㣩=77.5�㣬������ƽ�ǵĶ��弴�������CDE=180�㩁��CDA����EDB=180�㩁50�㩁77.5��=52.5�㣬�ʴ�ѡD��
D
��������������������ݵ��������ε������Ƴ���A=��CDA=50�㣬��B=��DCB����BDE=��BED�����������ε�������������B=25�㣬�������ε��ڽǺͶ��������BDE=��BED=��180�㩁25�㣩=77.5�㣬������ƽ�ǵĶ��弴�������CDE=180�㩁��CDA����EDB=180�㩁50�㩁77.5��=52.5�㣬�ʴ�ѡD��
һ�������ĺ�����װ��2�������1���������dz���ɫ�ⶼ��ͬ����������������һ����������������ȷ����(����)
A. ���������DZ�Ȼ�¼�
B. ���������Dz������¼�
C. ������������������Ŀ��������
D. �����������������Ŀ����Դ�
 D
����������������¼��ĸ���Լ��������ľ͵õ����������ֱ�������ɣ�
��������
A����������������¼����ʴ�ѡ�����
B����������������¼����ʴ�ѡ�����
C�������������������Ŀ�������ȣ�
���ݲ����ĺ�����װ��2�������1�����ó������������������Ŀ����Դʴ�ѡ�����
D�����ݲ����ĺ�����װ��2�������1�����ó��������������...
D
����������������¼��ĸ���Լ��������ľ͵õ����������ֱ�������ɣ�
��������
A����������������¼����ʴ�ѡ�����
B����������������¼����ʴ�ѡ�����
C�������������������Ŀ�������ȣ�
���ݲ����ĺ�����װ��2�������1�����ó������������������Ŀ����Դʴ�ѡ�����
D�����ݲ����ĺ�����װ��2�������1�����ó��������������... ��֪ij�ֲ�Ʒ�Ľ���Ϊÿ��40Ԫ�����ڵ��ۼ�Ϊÿ��60Ԫ��ÿ���ڿ�����300�����г����鷢�֣��ò�Ʒÿ����1Ԫ��ÿ���ڿɶ�����20�������ڹ�������ԭ���������ó���380���������ֲ�Ʒÿ������xԪ��xΪ��������ÿ���ڵ���������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���ò�Ʒ���ۼ۶�Ϊÿ������Ԫʱ��ÿ���ڵ��������������������Ƕ���Ԫ��
��3���ò�Ʒ���ۼ���ʲô��Χʱ��ÿ���ڵ�����������6000Ԫ����ֱ��д�������
 ��1��w=��20x2+100x+6000��x��4����xΪ��������2���ۼ۲�����56Ԫ�Ҳ�����60Ԫʱ��ÿ����������6000Ԫ��
�������������������1����������=���ۼ۩����ۣ������ۼ����������W��x֮��ĺ�����ϵʽ��
��2�������䷽����ú��������ֵ���Ӷ�����ô𰸣�
��3������ÿ���ڵ�����������6000Ԫ�в���ʽ��⼴�ɣ�
�������: ��1��w=��20��x����3...
��1��w=��20x2+100x+6000��x��4����xΪ��������2���ۼ۲�����56Ԫ�Ҳ�����60Ԫʱ��ÿ����������6000Ԫ��
�������������������1����������=���ۼ۩����ۣ������ۼ����������W��x֮��ĺ�����ϵʽ��
��2�������䷽����ú��������ֵ���Ӷ�����ô𰸣�
��3������ÿ���ڵ�����������6000Ԫ�в���ʽ��⼴�ɣ�
�������: ��1��w=��20��x����3... ����y=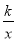 ��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
A. 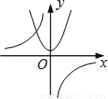 B.
B. 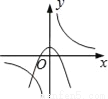 C.
C. 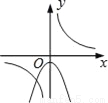 D.
D. 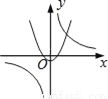
 B
��������Aѡ���У���������������ͼ������ô������Ӧ��y�ύ�ڸ����ᣬ����A�����ܣ�
Bѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����B���ܣ�
Cѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����C�����ܣ�
Dѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����D�����ܣ�
��ѡB.
...
B
��������Aѡ���У���������������ͼ������ô������Ӧ��y�ύ�ڸ����ᣬ����A�����ܣ�
Bѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����B���ܣ�
Cѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����C�����ܣ�
Dѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����D�����ܣ�
��ѡB.
... ��ͼ���ڵ�����ABC�У���A=80�㣬��B�͡�C��ƽ�����ཻ�ڵ�O
��1������OA�����OAC�Ķ�����
��2����BOC��
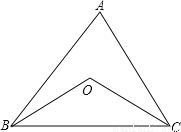
 (1) 40��;(2) 130��
�������������������1������AO�����õ��������εĶԳ��Լ�����á�OAC�Ķ�������2�����������ε��ڽǺͶ����Լ���ƽ���ߵĶ������BOC���A�Ĺ�ϵ���ٰѡ�A���뼴�����BOC�Ķ�����
���������
��1������AO��
���ڵ�����ABC�У���B�͡�C��ƽ�����ཻ�ڵ�O��
�������ABC�����߶�AO���ڵ�ֱ�߶Գƣ�
�ߡ�A=80�㣬
...
(1) 40��;(2) 130��
�������������������1������AO�����õ��������εĶԳ��Լ�����á�OAC�Ķ�������2�����������ε��ڽǺͶ����Լ���ƽ���ߵĶ������BOC���A�Ĺ�ϵ���ٰѡ�A���뼴�����BOC�Ķ�����
���������
��1������AO��
���ڵ�����ABC�У���B�͡�C��ƽ�����ཻ�ڵ�O��
�������ABC�����߶�AO���ڵ�ֱ�߶Գƣ�
�ߡ�A=80�㣬
... ��֪����ͼ���ڡ�ABC�У���ACB��90�㣬CDΪ�ߣ�CEƽ�֡�BCD���ҡ�ACD����BCD��1��2����ôCE��AB���ϵ����߶���?˵�����ɣ�
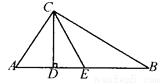
 ������
������������������������ACD=30�㣬��BCD=60�㣬Ȼ����ݽ�ƽ���ߵĶ��������DCE=��BCE=30�㣬�ٸ���ֱ������������ǻ��������B����A���Ӷ��õ���A=��ACE����B=��BCE�����ݵȽǶԵȱߵ����ʿɵ�AE=EC��BE=EC��Ȼ�����AE=BE�����ɵý⣮
���������CE��AB���ϵ����ߡ�
���ɣ��ߡ�ACB=90�㣬��ACD:��BCD=1:2��
��...
������
������������������������ACD=30�㣬��BCD=60�㣬Ȼ����ݽ�ƽ���ߵĶ��������DCE=��BCE=30�㣬�ٸ���ֱ������������ǻ��������B����A���Ӷ��õ���A=��ACE����B=��BCE�����ݵȽǶԵȱߵ����ʿɵ�AE=EC��BE=EC��Ȼ�����AE=BE�����ɵý⣮
���������CE��AB���ϵ����ߡ�
���ɣ��ߡ�ACB=90�㣬��ACD:��BCD=1:2��
��... ��ͼ����A����D��AC��DF����ô��Ҫ����һ��ֱ������________(д��һ������)������ʹ��ABC�ա�DEF��
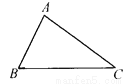
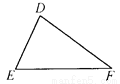
 AB��DE�����B����E���C����F��
����������������AB=DE��
�ڡ�ABC�͡�DEF�У�
��
���ABC�ա�DEF(SAS)��
������������B����E��
�ڡ�ABC�͡�DEF�У� ��
���ABC�ա�DEF(AAS)��
������������C����F��
�ڡ�ABC�͡�DEF�У� ��
���ABC�ա�DEF(ASA)��
�ʴ�Ϊ��AB=DE����...
AB��DE�����B����E���C����F��
����������������AB=DE��
�ڡ�ABC�͡�DEF�У�
��
���ABC�ա�DEF(SAS)��
������������B����E��
�ڡ�ABC�͡�DEF�У� ��
���ABC�ա�DEF(AAS)��
������������C����F��
�ڡ�ABC�͡�DEF�У� ��
���ABC�ա�DEF(ASA)��
�ʴ�Ϊ��AB=DE����... �ֽ���ʽ��x2(x��y)2��4(y��x)2.
 (x��y)2(x��2)(x��2)
�������������������ȡ����ʽ(x��y)2��������ƽ���ʽ��ʽ�ֽ⼴��.
���������
x2(x��y)2��4(y��x)2
=x2(x��y)2��4(x��y)2
=(x��y)2(x2��4)
=(x��y)2(x��2)(x��2).
(x��y)2(x��2)(x��2)
�������������������ȡ����ʽ(x��y)2��������ƽ���ʽ��ʽ�ֽ⼴��.
���������
x2(x��y)2��4(y��x)2
=x2(x��y)2��4(x��y)2
=(x��y)2(x2��4)
=(x��y)2(x��2)(x��2). �ӵ�����ֱ�����׳�һ��С��С��ĸ߶�h���ף����˶�ʱ��t���룩֮��Ĺ�ϵʽΪh=30t��5t2����ôС���׳� ���ﵽ��ߵ㣮
 3
����������������������������⣬�Ȱ�ʵ������ת������ѧ�����֪�������������h=30t��5t2�Ķ������꼴�ɣ�
��������
h=��5t2+30t��
=��5��t2��6t+9��+45��
=��5��t��3��2+45��
��a=��5��0��
��ͼ��Ŀ������£������ֵ��
��t=3ʱ��h���ֵ=45��
��С���׳�3���ﵽ��ߵ㣮
�ʴ�Ϊ��3��
...
3
����������������������������⣬�Ȱ�ʵ������ת������ѧ�����֪�������������h=30t��5t2�Ķ������꼴�ɣ�
��������
h=��5t2+30t��
=��5��t2��6t+9��+45��
=��5��t��3��2+45��
��a=��5��0��
��ͼ��Ŀ������£������ֵ��
��t=3ʱ��h���ֵ=45��
��С���׳�3���ﵽ��ߵ㣮
�ʴ�Ϊ��3��
... 
