不等式组﹣1＜x＜4的整数解有_________个．
4
【解析】在﹣1＜x＜4范围内的整数只有0，1，2，3，
所以等式﹣1＜x＜4的整数解有4个，
故答案为4． 若a＞c，则当m_________时，am＜cm； 当m_________时，am=cm．
＜0 =0
【解析】根据不等式的基本性质：不等式两边乘（或除以）同一个负数，不等号的方向改变，可知m＜0．
∵a＞c，
又知：am＜cm，
∴根据不等式的基本性质3可得：
m＜0；
又知：am=cm，
∴m=0．
故答案为：＜0；=0． 小于88的两位正整数，它的个位数字比十位数字大4，这样的两位数有_________个．
5
【解析】设十位数字为x，则个位数字为x+4
依题意得10x+x+4＜88
得x＜
又∵x应为正整数，且大于0；并且0≤个位数字≤9，因而5≤x+4≤9
∴1≤x≤5，故这样的两位数有5个．
故答案：5. 不等式组﹣1＜x﹣5＜11的解集是_________．
4＜x＜16
【解析】不等式每个部分都加5得，4＜x＜16．
故答案为：4＜x＜16． 若不等式组
有解，则a的取值范围是__________________.
a≤2
【解析】∵x≤2且x≥a，要使2者有公共部分,必须满足：a≤2.
∴a的取值范围是a≤2. 一次函数y=﹣3x+12中x_________ 时，y＜0．
＞4
【解析】根据题意得：﹣3x+12＜0，
解得：x＞4．
故答案为：＞4； 不等式x﹣8＞3x﹣5的最大整数解是_________．
﹣2
【解析】不等式x﹣8＞3x﹣5的解集为x＜﹣；
所以其最大整数解是﹣2． 直线l1：y=x+1与直线l2：y=mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为 ．
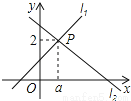
x≥1
【解析】
试题分析：首先把P（a，2）坐标代入直线y=x+1，求出a的值，从而得到P点坐标，再根据函数图象可得答案．
【解析】
将点P（a，2）坐标代入直线y=x+1，得a=1，
从图中直接看出，当x≥1时，x+1≥mx+n，
故答案为：x≥1． 解不等式，并把解集在数轴上表示出来：
（1）5x﹣6≤2（x+3）；
（2）
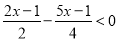
（1）x≤4； （2）x＞﹣1，
【解析】【试题分析】（1）根据解一元一次不等式基本步骤：去括号、移项、合并同类项、系数化为1可得；
（2）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．
【试题解析】（1）去括号，得：5x﹣6≤2x+6，
移项，得：5x﹣2x≤6+6，
合并同类项，得：3x≤12，
系数化为1，得：x≤4，
... 解不等式组：
（1）
；
（2）
．
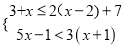（1）0＜x≤4；（2）0≤x＜2．
【解析】【试题分析】（1）分别求出每一个不等式的解集，根据口诀：大小小大中间找即可确定不等式组的解集；
（2）分别求出每一个不等式的解集，根据口诀：大小小大中间找即可确定不等式组的解集．
【试题解析】
（1）解不等式5x﹣6≤2（x+3），得：x≤4，
解不等式，得：x＞0，
∴不等式组的解集为0＜x≤4；
（2）解不...